Exploration of Graphs using Distance Formulas

Consider two point (3,4) and (-5,2). For any point (x,y) we can write the distance equations using a constant n.

Explore graphs with these two distance equations using Graphing Calculator 2.0. By using a slider variable n, the graph can be examined for non-zero constants.

The graph below represents the graphs of the equations if n=2.

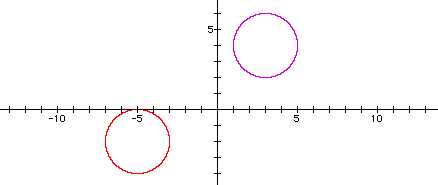
Where as the following graph represents the equation if n=5.

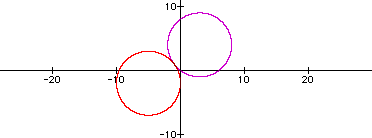
The next graph represents the equation if n=7.

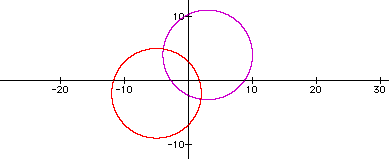
Once the graphs of the equations are observed using different non-zero constants, then consider the sum of the graphs.

This equation was graphed with the equation in order to make a visual comparison.

as n increases, the graphs appears more circular as when n=20

And even more circular as n gets larger for example, n=50

Now let's consider if we the product of the two equations.

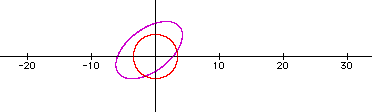
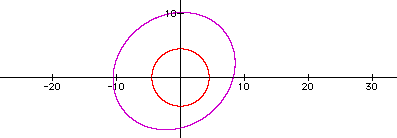
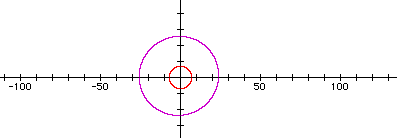
The product of the two equations give a different result. The blue graph represents the product of the two equations. The red graphs represent the circle and the purple represents the sum of the equations (n=27)

 

 

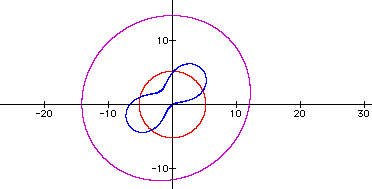
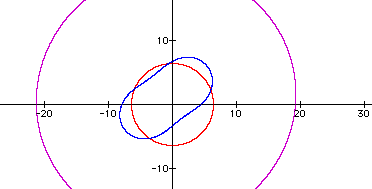
As n increases, the graph becomes more oval in shape. (n=42)

 

When n=25 a lemniscate appears.

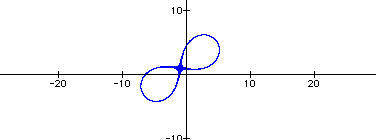
Using the graphing calculator software, I was able to view the different values of n while looking at both the product and the sum of the two equations using a unit circle as a standard.

Return