Graph ![]()
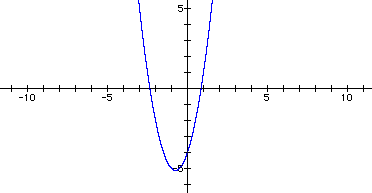
i. Overlay a new graph replacing each x by (x-4).
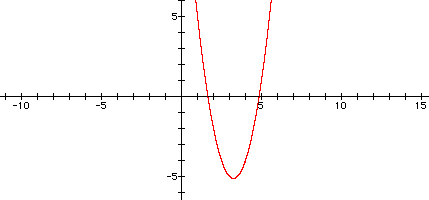
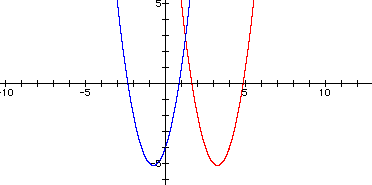
ii. The next part ask that the equation be moved into the second quadrant. The first solution path the I chose to substitute (x+4) in for x to see what would happen. This simply shifted the graph to the left 4 units.
Because we want a shift on the y axis, I used the graphing calculator software to add n to y and viewed the change of the graph.
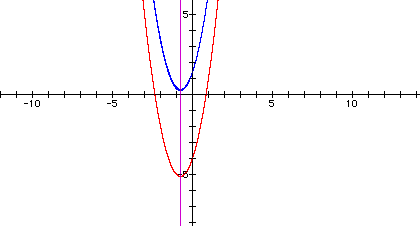
In order to move the graph into the second quadrant, the graph must be shifted up. This can be accomplished by adding any value of n such that n< -5.
The equation would be ![]() such that n<-5. At n=-5
the vertex would lie on the x-axis.
such that n<-5. At n=-5
the vertex would lie on the x-axis.
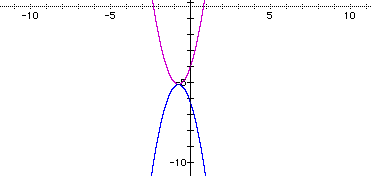
iii. The question was to produce the graph concave down using the same vertex.
In order for the parabola to open down, the coefficient of the square term need to be negative. To do this algebraically, I completed the square for the original equation.
With the equation in this format, the graph can be manipulated to be concave down by making the 2 negative.
The expanded form of the equation can be found easily using graphing calculator and the expand function.