Given line segments j, k, and m. If these are the medians of a triangle, construct the triangle.
Medial triangles are triangles formed by using the medians of a triangle to form the sides.
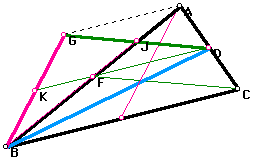
In order to work backwards, I first had to construct a medial triangle from Triangle ABC to look for a relationship between the triangle and its medial triangle. Some extraneous segments had to be added in order to form parallelograms.

Triangle ABC has medial triangle GDB. The ratio of the areas of the triangles is 0.75. The point F is the centroid of the medial triangle, J is the midpoint of segment GD and the length of BJ is 3/4 the length of AB. Segment AB is also the diagonal of parallelogram BCAE. By using this information, I was able to construct the triangle using the medians.
Constructing original triangle from medial triangle
The first step is to construct a triangle using the median segments given.
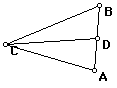
By trisecting CD, I was able to find the length of the segment CK.

Since CK is the diagonal of the parallelogram with side CA, point L is constructed.
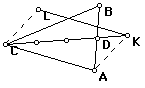
Segment LK is the median of the triangle, which makes L the midpoint of the segment with C as the endpoint. Therefore, by constructing a segment congruent to CL, I found another side of the triangle.
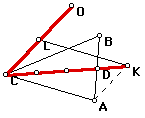
The third side of the triangle is found by connecting points K and O.
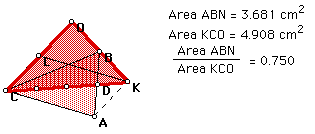
I measured the ratios of the areas of the triangles to find the ratio to be 0.75. The triangle has been constructed using the medians.
Triangle COK is the triangle formed by its median.
Return to Home Page
Return to Final project