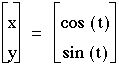
Curves that are not graphs of functions can often be specified by using a pair of equations x=x(t) and y=y(t) to express the coordinates of a point (x,y) on the curve as functions of an auxiliary variable t. These are called parametric equations for the curve, and variable t is called a parameter. Parametric equations arise naturally if one imagines a plane curve C to be traced by a moving point. If we use the parameter t to denote time, then the parametric equations x=x(t) and y=y(t) specify how the x- and y-coordinates of the moving point vary with time.
Examine some parametric equations by graphing the following on an appropriate software package such as Algebra Xpressor or Graphing Calculator 2.0 (or more current).
1) 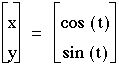
2) 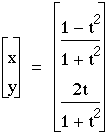
3) 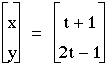
Click here to check your graphs.
What did you notice about the last parametric equation you graphed? Was it a curve?
By choosing a range of values for t, the resulting x and y values form ordered pairs that can be graphed on a coordinate plane to illustrate the equation. Following this philosphy, it seems reasonable to assume that just about anything can be written in parametric equation form and graphed, even if the equation's graph is a line.
Write a parametric equation of a line through (7,5) with a slope of 3. Graph the line using your equations.
First consider forming an equation from the information
using the slope formula and the point (7,5). Then, 3/1 = (y-5)/(x-7). A
cross product yields 3x-21=y-5. Solving for y gives the two-variable linear
equation y=3x-16. Next, it would be helpful to use a table of values to
form some ordered pair solutions to the equation. These are (0,-16), (1,-13),
(2,-10), (3,-7), (4,-4), and so on. To represent these ordered pairs in
parametric equation form, we need to consider an equation in t that would
give the appropriate x values and an equation in t that would also give
the appropriate y values. This should happen as the same value of t is used
for both the x and y equations. If we let x = t, then as t goes from 0 to
4 produces the needed x-coordinates of 0,1,2,3, and 4. What would be the
equation for y so that as the same value for t is plugged in to the x equation
it will also give the needed y-coordinate. Well, using the equation found
earlier (y=3x-21), all we need to do is to place t in for x giving the y
equation y=3t-21. These two equations can be written in the following parametric
form: 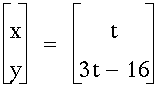
As a value for t is plugged into each equation for x and y, the resulting ordered pairs match those found for the original linear equation. Furthermore, when the new parametric equation and the original equation are graphed on the same set of axes, they are indeed the same line. (see picture below)
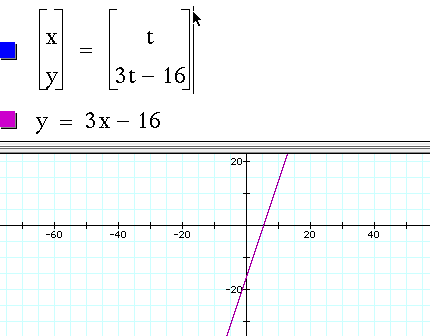
Can you write a parametric equation for some other types of equations?
Try to write a parametric equation of a line through (-2,4) with a slope of -3.
Click here to check your answer.
Return to home page.