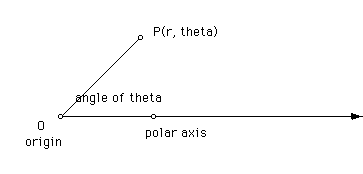
To form a polar coordinate system in a plane, pick a fixed point O called the origin or pole. Using the origin as an endpoint construct a ray called the polar axis. After selecting a unit of measurement, we may associate with any point P in the plane a pair of polar coordinates () where r is the distance from P to the origin, and measures the angle from the polar axis to the line segment OP (see figure). The number r is called the radial distance of P and is called a polar angle of P.

The distance from a point on a conic to a vertical line p can be expressed as . If a conic graph is a distance r from the focus and a distance kr from a directrix, this yields . Furthermore, solving for r gives the following polar form of a conic equation:

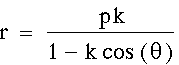
Explore the basic polar form of conics by graphing several equations using the graphing software tools Algebra Xpressor or Graphing Calculator 2.0. Also investigate with different values of p for k>1, k=1, and k<1. For example, using the above polar conic form with p=1 and k=1 gives the following graph:

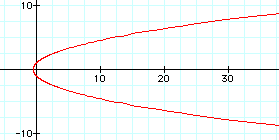
With k=1, the graph is a parabola. What would a different value for p, such as p= 5, do to the graph of the parabola?

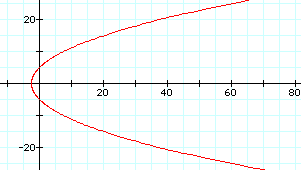
Notice the parabola seems wider. What about when p=1/4? Can you predict what the graph might look like now?

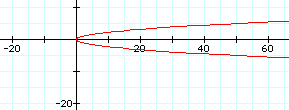
The graph has indeed become "skinnier". What do you think will happen if p is a negative number?

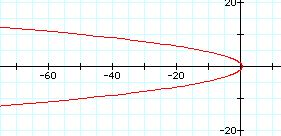
Obviously a reflection across the y-axis has occurred. Next, explore the graphs when k<1 and k>1. Describe your findings, and be sure to tell what happens as the values of p are varied.

1) a. k<1 and p=1 is the graph of __________________________.

b. Describe changes in the graph when p=5, p=1/4, and when p is negative.

p=5 _________________________________________

p=1/4 ________________________________________

p=-1 __________________________________________

2) a. k>1 and p=1 is the graph of _________________________.

b. Describe changes in the graph when p=5, p=1/4, and when p is negative.

p=5 _________________________________________

p=1/4 ________________________________________

p=-1 __________________________________________

Click here to check your response to 1a and 2a.

Another interesting investigation could result from substituting sine in for cosine in the equations. How does this affect the graph of the conics?

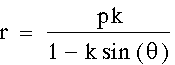
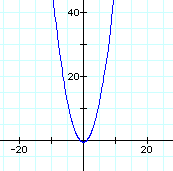
The sine value creates a parabola that opens vertically up!!! Once again the exploration of p values and k values might yield patterns and observatons that are interesting. How does this graph for p=1 and k=1 compare to the graph of the more familiar equation Can you draw any conclusions or make any connections relating the polar form of conics with the two varible x and y form?

Click here to return to home page.