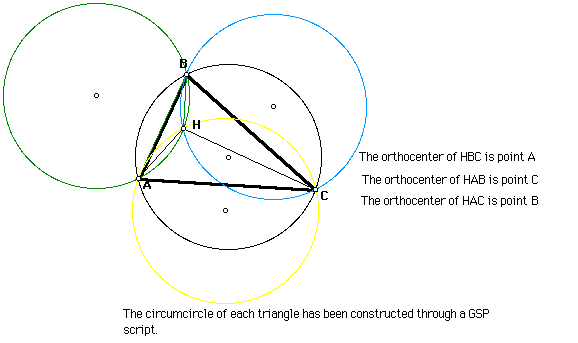
The following constructions should be done on the Geometer's Sketchpad (GSP).

1) Construct any triangle ABC.

2) Construct the Orthocenter H of triangle ABC.

3) Construct the Orthocenter of triangle HBC.

4) Construct the Orthocenter of triangle HAB.

5) Construct the Orthocenter of triangle HAC.

6) Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

The resulting figure should match the above constructions:

Do the following:

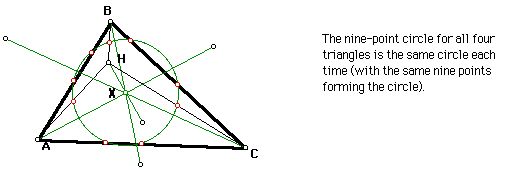
Construct the nine-point circles for triangles ABC, HBC, HAC, and HAB. The nine-point circle is the circle connecting the midpoints of the sides of the triangle, the feet of the altitudes of the sides, and the midpoints of the segments from orthocenter to the vertices. The center of the nine-point circle is the midpoint of the orthocenter and the circumcenter.

The following GSP sketch illustrates the result of finding the nine-point circles.

Click here for a GSP script that will construct the nine-point circle of a triangle.

As a student, make some conjectures or draw some conclusions as to why the circle was the same for not only the original triangle, but for the three interior triangles created from the orthocenter of the original triangle. Hint: Note that in the first sketch above the orthocenter of each interior triangle is a vertex of the original triangle.

Return to Home Page.