The sums of the square of the sides of a right triangle is equal to the square of the hypotenuse.
Objective: To develop an understanding of Pappas'
theorem on areas of parallelograms formed by the sides of any
given triangle. This essay was designed to be understood by high
school geometry students following lessons on the Pythagorean
Theorem.
Many are familiar with the Pythagorean Theorem.
The sums of the square of the sides of a right triangle is equal to the square of the hypotenuse.
Given triangle with legs a and b, with hypotenuse c,
Illustrate this theorem.
The Pythagorean Theorem applies only to right triangles. Verify this necessary condition by experimenting with different
triangles.
From your experiments, you should have seen that
the Pythagorean Theorem only applies to right triangles. In the
illustration, squares were created from the sides of the triangle.
Squares have specific properties. All sides and angles must be
congruent.
Since squares formed by the sides of a right triangle have a relationship,
could a relationship be made with another polygon with acute or
obtuse triangles? A question that mathematicians such as Pappas
must have considered was 'what if we chose a polygon with fewer
restrictions?'
Pappas of Alexandria (320 A.D.) wrote a
generalization of the Pythagorean Theorem in Collections.
Just as the Pythagorean Theorem was known prior to Pythagoras,
the concept of this Pappas area may not have originated with Pappas,
but earlier with Heron. For simplicity sake, we will refer to
the generalizations of the Pythagorean Theorem as Pappas Area
Theorem.
In his writing, Pappas constructed the following:
Given any triangle ABC, construct parallelograms on two of the sides of the triangle. Then construct a third parallelogram on the third side equal to the sum of the other two parallelograms.
The measurements above are simply
examples. The parallelograms can have different areas, but they
will always have the same relationship. Experiment with these
parallelograms.
In the examples above, the third parallelogram was constructed
for you. How do you construct the third parallelogram to equal
the sum of the other two parallelogram?
First, find the intersection of the lines containing the side
of the constructed parallelograms opposite the sides of the original
triangle. Draw the segment that connects this intersection point
to the vertex of the original triangle common to both constructed
parallelograms. This segment act as a vector to determine the
length and direction of the third parallelogram. The sides of
the third parallelogram will be congruent and parallel to this
segment/vector.
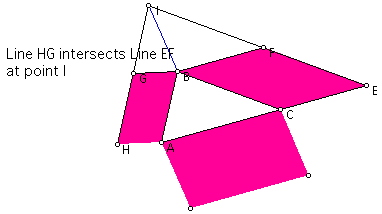
The segment or vector that determines the side
of the third parallelogram is IB.
We can once again return to the Pythagorean Theorem
to examine the vector used to form the third parallelogram.
The Pythagorean Theorem uses the sides of the triangle and altitude
of the triangle to determine the square of the third side. The
sides of the triangle are the bases. If we placed the picture
on the coordinate grid, the altitude of the square on the hypotenuse
can be found using the distance formula.
Using substitution , the distance formula is equivalent to the formula used for the Pythagorean Theorem. Let a=altitude and b=base so d would represent the hypotenuse.
For an illustration of the formulas using squares and parallelograms,
click on each highlighted word.
Now that we have examine the length of the vector
that determines the third parallelogram, let's look at the areas
of the parallelograms.
The area of a parallelogram is equal to the length of the
base times the length of the altitude or height. The area of the
parallelogram does not change as long as the length of the base
and the altitude remain the same.
To shear a parallelogram means to translate a side along
the line that contains the side. Illustrate shear.
The shear can occur with any side of the parallelogram, as long
as the side moves along the line parallel to the opposite side.
Another side of the parallelogram can also be sheared.
The GSP sketch of Pappas Area is a sequence of
translations. Shearing the parallelograms involve translating
the sides of the parallelograms along the corresponding parallel
sides. The third parallelogram is then translated up along the
same parallel lines shared by the sides of the previously sheared
ones.
The translated parallelogram overlaps the original triangle which
is translated by the given vector to completely cover the two
parallelograms. This translation is possible because the original
triangle does not overlap the two sheared parallelograms.
Pappas Area Theorem is illustrated by a GSP
sketch. There are three choices to show transformations. Choose
one or all to illustrate Pappas
Area.
The sum of the areas of the parallelograms
formed on two sides of a triangle are equal to the area of the
third parallelogram with the sides formed by the resulting vector
of the intersecting parallel lines of the first two parallelograms
and their common vertex.
An algebraic view
If the area of the parallelogram does not change if the parallelogram is sheared, let's look at the figure with the parallelograms sheared.
The parallelograms HEAC and IEAB share a common side. HC = EA = IB
The side of the third parallelogram
is determined by EA, so 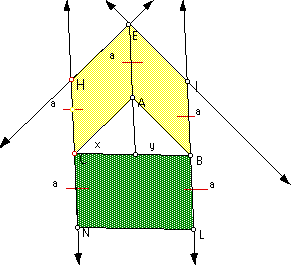 EA
= CN = BL
EA
= CN = BL
EA has length a.
x is the altitude of HEAC
y is the altitude of IEAB
Area of HEAC = ax
Area of IEAB = ay
Area of CBNL = a(x + y)
= ax + ay
Therefore, Given any triangle, the area of third parallelogram
is equal to the sum of the two parallelograms formed by the sides
of the triangle.
Pappas in 3-dimensions
I thought it might be interesting to observe Pappas Area in a
3-dimensional setting. Although the sketches are limited, the
generalization is still applicable to the figure that was sketched.
That figure was a tetrahedron.
A tetrahedron is a solid that has four triangular faces. The tetrahedron
was constructed with an equilateral triangle. A prism was constructed
on each face. Each prism has three parallelograms as faces which
would form its lateral surface area.
Click 3-D to view Pappas in 3-dimensions.
Two possibilities occur when working with parallelograms 3-D. Any two adjacent prisms can be viewed. The adjacent faces of two prism are parallelograms. These parallelograms can be used to determine a third parallelogram that would lie on the plane formed by the outside edges of the prism.
Click here to illustrate.
The second possibility occurs when working with a singular prism. The area of the third parallelogram face of a prism will equal the sum of the areas of the other two parallelogram faces.
For this sketch I made one prism, then I constructed the prism such that the parallelogram faces would lie on the same plane. When the parallelograms are coplanar the previous explanations of Pappas Area Theorem are easily applied.
Click here to illustrate.
In the previous sketch, although I may have started with an equilateral triangle in my original design, by moving the vertices, the triangle may be changed. This would lead to a conjecture that Pappas Area Theorem can be applied to any triangular figure. What an interesting extention of this assignment to be considered.