Objective of Essay:
Most high school geometry students construct
and examine points of concurrency associated with triangles. Students
can use a compass and straightedge, geometry software, or paper
folding to construct the incenter, circumcenter, orthocenter,
and centroid. Many students even construct and discuss the Euler
Line.
On the other hand, students rarely hear of Gergonne's point. Many
high school geometry teachers would be unable to identify it if
asked. Therefore, I thought it would be good exploration. It would
also reinforce previously learned theorems and postulates for
geometry students as well as make connections to algebra.
This essay was designed for high school geometry
teachers to use in order to enhance their current curriculum.
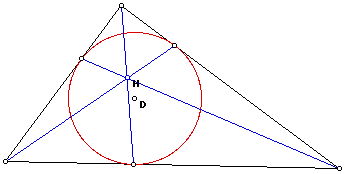
The Gergonne Point is the point of currency formed by the lines
containing the vertex of a triangle and the point of tangency
with the inscribed circle.
In order to construct the Gergonne Point, draw any triangle. Construct
the angle bisectors of each vertex. The intersection of the angle
bisectors form the incenter, or the center of the inscribed circle.
In order to construct the inscribed circle, construct a perpendicular
line from the center of the circle to the sides of the triangle.
At the point where the radius of the circle and the side intersect
is called the point of tangency. To complete the construction,
draw segments connecting the vertices of the triangle to the points
of tangency on the opposites of the triangle.

Does every triangle have a Gergonne Point?
The first question I raised was how do we know that this point
will always exist? Will the lines be concurrent with any triangle?
I first approach the question using Geometer's Sketchpad. By forming
a random triangle, I constructed Gergonne's point. Then, by using
the selection tool, I randomly translated each vertex to see whether
the lines remain concurrent.
Click here for GSP sketch
Postulates applied to GSP
Most geometry students are familiar with the
segment addition postulate.
C is between A and B if AC + CB = AB
By using the Geometer's Sketchpad, the segment lengths may be
viewed as the vertex is moved. A table is also available for a
sample of lengths of the segments for various triangles.
Click here for GSP sketch
Coordinate Geometry
The next approach that would be addressed in a geometry class would be using coordinate geometry. Students can construct a triangle on grid paper and use the point slope form of a line to write equations of the line segments. Since this process can be time consuming, GSP is recommended. By placing a grid on the sketch, an equation for each of the lines can be found by using the slope and the y intercept of each segment.
Equation were developed for the segments that appear to intersect inside the circle.
Using Algebra Xpresser, the lines can be graphed to find a solution. If there exist a solution or intersection for the three equations, then the lines are concurrent.
As you can see on the graph of the lines, although the lines do intersect in pairs and those two intersection points are very close to each other, there is no one intersection point. It is important to consider that the method used to obtain the slope and y-intercept require the software to make an approximation for the points when the coordinate graph is placed on the existing sketch. The calculations are not exact since it appears that the values are rounded to the nearest hundredth of a point. Randomly placed points rarely have such neat values.
This would be a wonderful example to return to at the end of the discovery to show the importance of exact values. Although it is not necessary in most lessons in GSP for the values shown to the user to be exact, exact values are crucial in areas of engineering and design where the computer programs are written for more accuracy in their display.
Another
Theorem?
An interesting theorem to discuss with a geometry class that reinforces algebra and solving proportions is Ceva's Theorem. This theorem is also an excellent way to show the Gergonne Point exist for all triangles.
Ceva's Theorem - The three lines containing the vertices A, B, and C of Triangle ABC and intersecting the opposite sides at points X, Y and Z, respectively, are concurrent if and only if
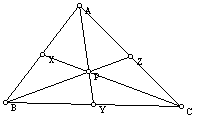
Learn more about the Theorem of Ceva.
The Ceva and Gergonne Connection
Once again returning to a previous sketch of the Triangle ABC with the Gergonne Point H, find the ratio of the measure of the segments.
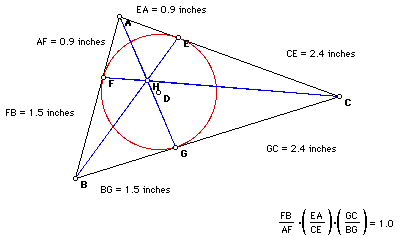
In order to change the size of the triangle and examine if the ratio remains the same experiment with diagram click here.
The Ceva Application
We can prove that the ratio remains the same by using the incenter and congruent triangles. This is possible because the segments necessary for the ratios are the same regardless of whether segments are drawn from the incenter (the radius of the circle) or from the segments used to form the Gergonne Point. By definition, both segments contain the point of tangency of the inscribed circle.
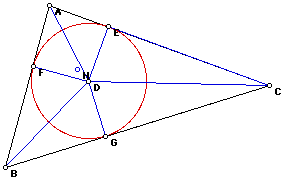
The statements that could be used in a formal proof are listed below.
Finally,
Corresponding Part of Congruent Triangles are congruent so GC = CE and GB = BF and FA = AE , therefore
A simple proof
The statements just discussed are used in high school geometry to prove theorems concerning line segments associated with circles.
Another way to prove the ratio of the segments equals one regardless of the size of the triangle is by applying this theorem frequently found in high school geometry books.
The segments AE, FA, BF, GB, CE and CG are tangent segments to circle D. By applying the theorem, two tangent segments to a circle from a common exterior point are congruent,