What happens when we start with a quadratic function in the form of

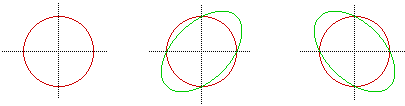
and very a from negative numbers, to zero and positive numbers? Most students will recognize the equation, when a is set equal to zero as the equation of a circle with a center at (0,0) and a radius of 3. This is the red circle in the graph below, to the left. The center graph has

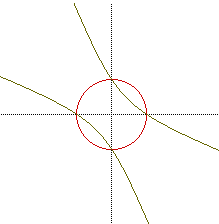
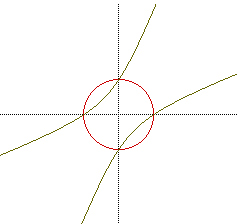
with two values of a, both 0 and -1. The graph to the left has values of a of 0 and +1.


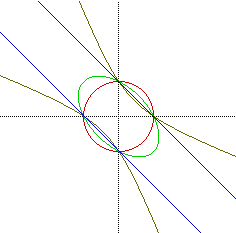
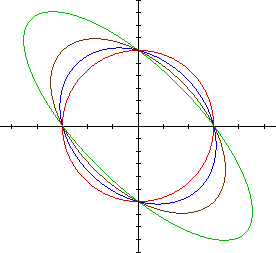
From examining the graphs with a equaling +1 and -1, we observe that they appear to be ellipses. By trying fractional values of a from -2 to 2, we can see more evidence that supports this observation. The larger the absolute value of a, the flatter the ellipse becomes. The following graph has been enlarged to make it easier to see the changes to the graph when a changes. The values of a range from O for the red circle to 1/2, 1, and 3/2 for the green ellipse.

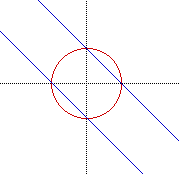
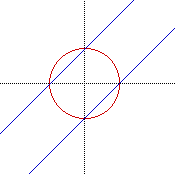
When we graph the equation with values of a as 2 (graph to the left) or -2, two straight lines appear.

How do we know that these are straight lines? By examining

with a =2, we notice that it can be factored as (x+y)(x+y)=9. If we take the square root of both sides, the result is that x+ y = 3 or x + y = -3. Both of these are equations of a line, and are in fact the lines that were graphed.

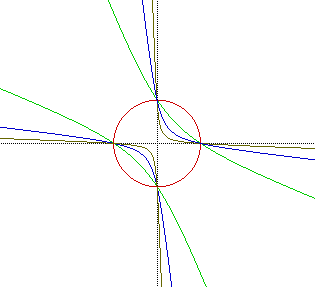
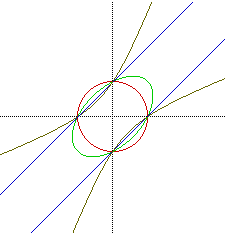
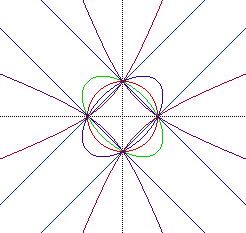
When the absolute value of a is increased to be greater than 2, a fourth type of graph appears, the graph of a hyperbola. As a increases, the hyperbola gets narrower and narrower, with its asymptotes appearing to approach the two axis.



The graph below shows the effects of changing a from values of 0 for the red circle to 3 to 9 to 29 for the brown hyperbola.

The following two graphs show how the graphs change when a changes from a positive to a negative value.


The last graph simply shows all the graphs, for seven different values of a.




A question that remains, and will be left for you to consider, is what happens to the graphs if a different constant other than nine is used in the original equation. Does the constant have to be a square number? Does it have to be an integer? Does it have to be positive?

Return to Lars' student page
Return to EMT 668 Page