 |  |
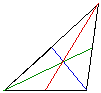
Triangles can be constructed in many shapes and sizes. A specific example
is one that is a triangle constructed from the medians of another triangle.
The black triangle below has its medians drawn in colors. The red, green
and blue triangle is the triangle constructed from the red, green and blue
medians respectively.
 |  |
All of the triangles in this write up were constructed using Geometer
SketchPad 3.0 (GSP). Triangle is a GSP document
that can be used to explore the relationship between a triangle and the
triangle made up of its medians.
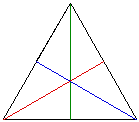
There is a relationship between an equilateral triangle and its triangle
made up of medians. Both triangles are equilaterals, as seen below. Here
is a GSP document that can be used to explore
the relationship between an equilateral triangle and the triangle made up
of its medians.
 | 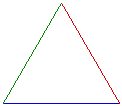 |
The ratio between the length of the side of the original triangle and
the median is a constant, with a value of 0.866 as measured by GSP. The
value of this ratio can be found algebraically using the pythagorean theroem.
If we look at the right triangle below, the black side is an original side
of the equilateral triangle. The green side is a median of the original
triangle, while the aqua side is one half of an original side. Using the
pythagorean theorem, we can calculate the length of the green side to be
![]() times the length of the original side.
times the length of the original side.
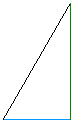
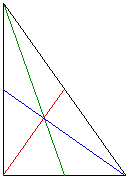
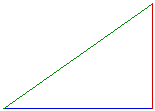
What happens when we have a right triangle, will the resulting triangle
made up of its medians always be a right triangle as well? By looking at
many different pairs of triangles, it is obvious that the resulting triangle
does not have to be a right triangle. There is one case when resulting triangle
is a right triangle and it is shown below. Here is a GSP
document that can be used to explore the relationship between a right
triangle and the triangle made up of its medians.
 |  |
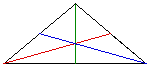
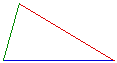
A third set of triangles that can be examined are the isosceles triangle
and the triangle made up of its medians. Using the measurement functions
of GSP, it can be determined that the resulting triangle is also an isosceles
triangle.
 |  |
Here is a GSP document that can be used to
explore the relationship between an isosceles triangle and the triangle
made up of its medians. During the animation of A, the vertex on the original
triangle where the green median is located, it appears that the resulting
triangle is not an isosceles triangle. The ratio between the red and blue
sides is only 0.99 instead of 1.00 at times within the animation. The same
ratio can not be found when point A is manually moved. This leads me to
believe that there is a bug within GSP.