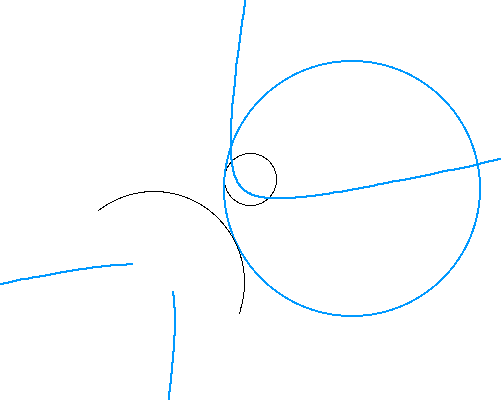Circles Tangeant To Objects
We will examine the relationship between circles tangeant to other circles,
circles tangeant to a circle and a line, and circles tangeant to a circle
and arc. Click on any picture to jump to that investigation.
When we are given two objects,
we can construct circles that are tangeant to the objects. The first example
that will be investigated is a circle tangeant to two other circles. We
can construct multiple tangeant circles, but there will be two sets of circles
as seen below. To examine the relationships between the circles, using Geometer
SketchPad, click here.
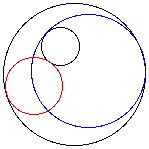
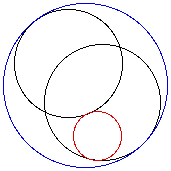
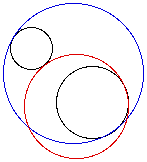
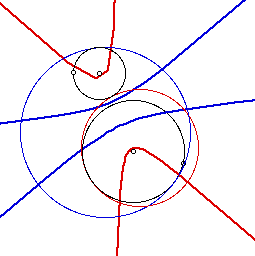
When the center of the tangeant circles is traced, as the point of tangeancy
is moved about the original circles, we get several different shapes. When
one circle is within the other cirle, we get ellipses. If the two circles
intersect, an ellipse and hyperbola are obtained while two hyperbolas are
obtained when the two circles are completely external to each other. Examples
of each are shown below, with the thicker line being the locus of the center
of the seame colored circle.

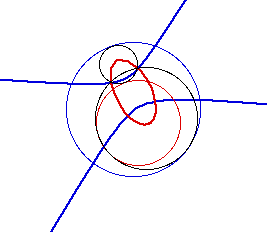
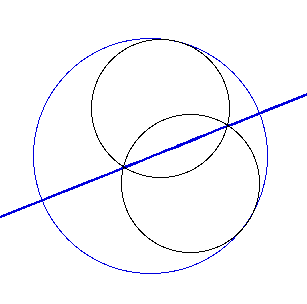
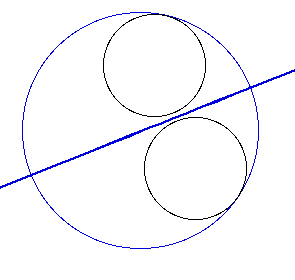
There are several interesting results when the circles have the same
radii. The blue locii that were hyperbolas, merge into one straight line.
This occurs for both cases that have two discrete circles with the same
radii., as seen below.
Click here for a GSP
script that will create a tangeant circle to other circles.
A circle can also be constructed
that is tangeant to a circle and a line.To examine the relationships between
the circles and a line, using Geometer SketchPad, click
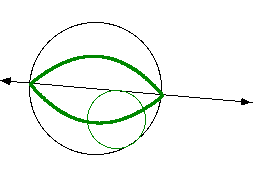
here. The thick green line is the
locus of the center of the circle that is tangeant to both as the point
of tangeancy is moved around the circle. Two parabolas are created by this
method, as seen below.

When the original circle and line intersect each other, the two parabolas
intersect as well.

When the center of the circle is on the line, the locus is symmetrical,
as shown in the diagram to the right.
Circles tangeant to a circle
and a line.To examine the relationships between the circles and an arc,
using Geometer SketchPad, click here. When first constructing the locus
of tangeant circle, I expected the ratio of the partial locus to the full
locus to be same as the ratio of the arc to a full circle. As seen below,
this is not the case, and the locus behaves differently from when constructed
with two circles. It can be seen that the shape of the locus varies depending
upon the length, and degrees that it covers.

To go to a library of GSP scripts, click
here.
Return to Lars' student page
Return to EMT 668 Page