A Triangle and its Circles

For any given triangle, multiple circeles can be created that are related to the triangle. The relationship between the incircle, three excircles and nine-point circle for a triangle will be examined. A scalene triangle will be examined, followed by several specific triangles including the equilateral, isosceles, and right triangles. Click on any of the four triangles to jump to the investigation of that type of triangle.

Scalene

Equilateral

Isosceles

Right

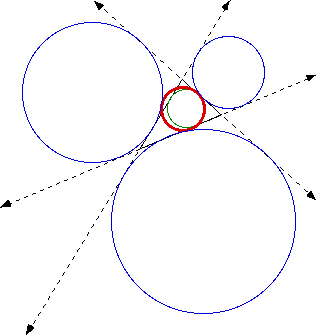
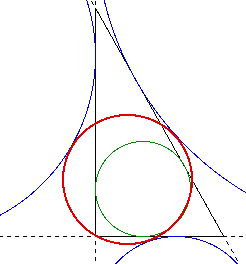
To help with the diagrams in the following investigations, the colors and line styles will be kept consitent. The original triangle has solid black sides. The excircles of a triangle will be blue, while the incircle will be green. The nine-point circle is red. The sides of the triangles have been extended as dashed lines. An example diagram follows.

All five of the circles are tangeant to at least one other circle. The nine-point circle is always tangeant to each of the excircles and incircle. The following diagrams show for an obtuse and acute triangle, that the nine-point circle is tangeant to each of the four other circles.

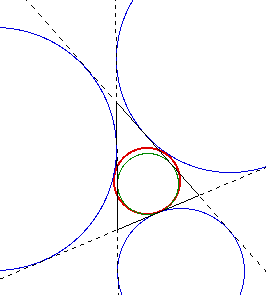
Depending upon the configuration of the triangle, the incircle can be tangeant to one or more of the excircles as well. The following diagram shows that the incircle can be tangeant to the nine-point circle and one of the excircles.

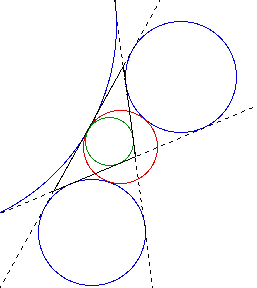
Through trial and error, it can be shown that the the nine-point circle and incircle can become the same circle. It appears that the triangle shown is an equilateral triangle. Equilateral triangles will be examined next to see if this holds true for a triangle that is constructed as an equilateral triangle.

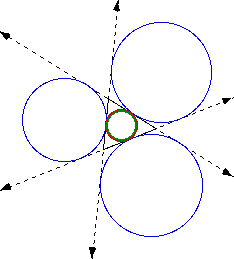
To examine the five circles for a triangle using GSP, click here.

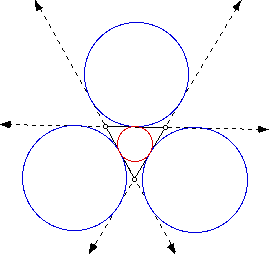
When an equilateral triangle is constructed, the incircle and nine-point circle are the same circle. The two circles are shown as the red circle in the diagram below. It should be noticed that the nine-point circle, incircle and excircles are tangeant at midpoint of each side. As the triangle is changed, this relationship stays true.

To examine the five circles for an equilateral triangle using GSP, click here.

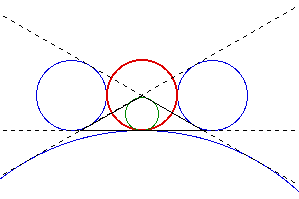
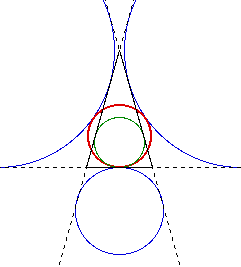
When an isosceles triangle is created with its five circles, the relationship that exists is different from the realtionship between an equilateral and its five circles. The nine-point and incircle are tangeant to an excircle at the midpoint of the base.

To examine the five circles for an isosceles triangle using GSP, click here.

The last special triangle to be examined is a right triangle. The nine- point circle and three excircles are always tangeant at one point for a right triangle. A different result from when we looked at the equilateral and isosceles triangle, the tangeancy point does not have be tangeant to one of the sides of the triangle for any of three excircles. This can be seen in the diagram below.

To examine the five circles for a right triangle using GSP, click here.

To go to a library of GSP scripts, click here.

Return to Lars' student page

Return to EMT 668 Page