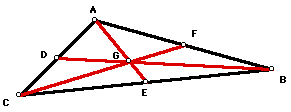
The Centroid:
The centroid of a triangle is the point of intersection of the medians of the sides of a triangle. No matter how the triangle is transformed, the three medians will alway intersect in this single point. In this example G, the centroid of triangle ABC, is the point of intersection of the three medians AE, CF and DB of the triangle.

The Circumcenter:
The circumcenter of a triangle is the center of a circle in which a triangle is inscribed. In this example, triangle ABC is inscribed in circle D. The circumcenter of triangle ABC is D. Notice that since AD, BD and CD are radii of the circumscribed circle they are all the same length.
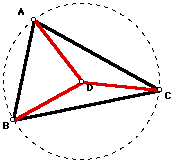
The Incenter:
The incenter of a triangle is the center of a circle inscribed in a triangle. It is also the intersection of the three angle bisectors of the triangle. In this case D, the incenter of triangle ABC, is the center of the circle inscribed in triangle ABC.
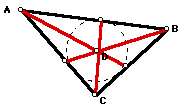
The Orthocenter:
The orthocenter of a triangle is located at the common intersection of the three altitudes of a triangle. In this case G, the orthocenter of triangle ABC, is located at the intersection of the altitudes: AD, EB and FC.
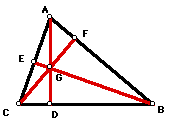
The Euler Line:
Here are all four incenters (CC: Circumcenter, CE: Centroid, IC: Incenter, OC: Orthocenter) for the same triangle.
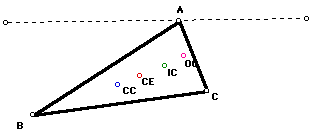
By animating the vertices along various lines and tracing the paths of the four centers, it turns out that these centers trace the conics.
The orthocenter, centroid and circumcenter are colinear for all triangles. For isosceles triangles, all four centers are collinear.
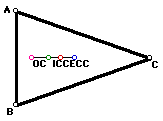
In the case of the equilateral triangle, the four centers coincide.
Napoleon's Theorem:
Beginning with the arbitrary triangle determined by free points A, B and C, one can find the outer Napoleon triangle of triangle ABC. First construct the three equilateral triangles AHC, BDA and BMC and their respective centroids L, G and Q as shown at right. Connecting the three centroids forms the triangle GQL known as the outer Napoleon triangle of triangle ABC. It appears that triangle GQL is equilateral. Dragging the vertices and sides of triangle ABC through a variety of positions helps to confirm the conjecture that no triangle GQL will always be equilateral for any given triangle. One might conjecture from this investigation that Napoleon's Theorem goes something like the following: "Joining the bases of three equilateral triangles and connecting their centroids will always form a fourth equilateral triangle."
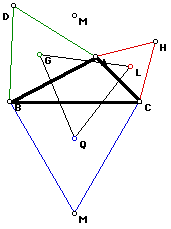
Constructing segments connecting each vertex of the original triangle ABC with the most remote vertex of the equilateral triangle GQL on the opposisite sides, one sees that the three segments intersect in a common point.
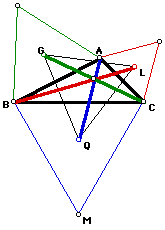
By reflecting each centroid across its corresponding edge in the original triangle, one can construct the inner Napoleon triangle. Comparing the areas of the original triangle ABC and the outer and inner Napoleon triangles GQL and G'Q'L' one can see that the area of the original triangle falls between the areas of the inner and outer Napoleon triangles.
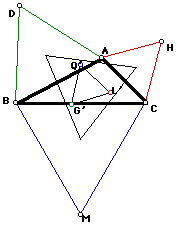
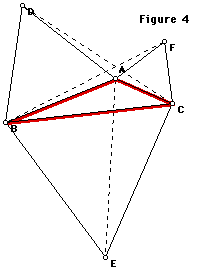
Fermat's Point:
The Power Plant Problem: Finding Another Center of a Triangle
Objectives:
1. Students will be challenged to explore triangles beyond the traditional concepts.
2. Students will see a real world application of triangles.
Materials:
Computers equipped with GSP
Discussion:
In this activity, students will investigate the Fermat point of a triangle. This is the unique point inside a triangle where the sum of the distances from the vertices is minimized. Using GSP they will explore this point in relation to the construction of a power plant. This activity helps students explore a concept that it not taught in most mathematics classrooms but has important real world applications. Using GSP allows the students to investigate a variety of situations in order to form conjectures and argue conclusions.
Activities:
A power plant is to be constructed to serve three cities. The power company wants to minimize the amount of high-voltage cable used to deliver the electricity to each of the cities. Where should the power plant be built? (Assume that the three cities do not lie in a straight line, and that the high-voltage power lines can be run in straight lines from the power plant to each city.) Work with your partner to construct a model using GSP.
How could you find the location of the power plant using geometry?
Is this point (where the power plant should be located) the same no matter where the cities are located? Move one of the cities (the points) to see.
In one particular situation, a power plant is being built to serve cities A, B, and C. See figure below. The mayor of city A claims that the power plant should be built at the center of city A. Test the mayors claim. Is he right? Why or why not?

Work with your partner to construct a model that would work for any three arbitrary cities. Why does your model work?
Discuss this problem and your findings. Complete a write-up including your models.
Assessment:
Complete a write-up of your findings. Include your GSP sketches.
Here's an example of what I would like to see students create:
A power plant is to be constructed to serve three cities. The company wants to minimize the amount of high-voltage cable used to deliver the electricity to each of the cities. Where should the power plant be built? (Assume that the three cities do not lie in a straight line, and that the high-voltage power lines can be run in straight lines from the power plant to each city.)
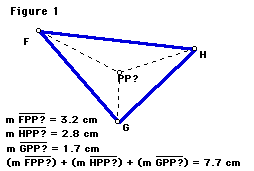
Using the three cities as vertices of a triangle, we can create a free point in the triangle and measure the distance from this point to each vertex (See figure 1). After calculating the sum of these distances, the free point can be translated to minimize the sum. At this point where the sum is minimized, the power plant should be located in order to minimize the amount of high-voltage power lines used.
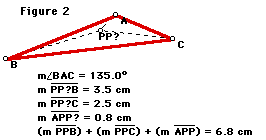
In the particular situation presented in figure 2, a power plant is being built to serve cities A, B, and C. The mayor of city A claims that the power plant should be built at the center of city A. As the free point PP? approaches A it appears that sum of the distances between the power plant and the three cities approaches a minimum value. The mayor of city A is apparently correct. If the angle BAC is changed, one can see that this is not true for every triangle. So how would one construct the point where the power plant should be given any triangle?
Using the three sides of triangle ABC as bases construct the equilateral triangles ABD, BCE and CAF. Connect the outlying vertices of the equilateral triangles to the opposite vertices of the original triangle ABC (See figure 3). The point where these three segments intersect (known as the Fermat point) is the point which minimizes the sum of the distances from the vertices to a point within their triangle.
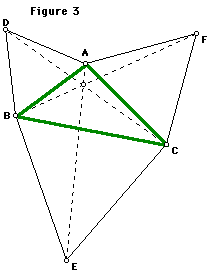
Utilizing this method on the power plant problem further confers that point A should be the location of the power plant proving that the mayor was right.