
Activity Sheet (1 per group)
Sno-cone Cups or Paper Plates (2 per group)
Construction Paper (1 sheet per group)
Stapler (1 per group)
Scissors (1 pair per group)
Discussion of Lesson:
The teacher will begin the lesson
by placing the list of knowledge from the previous lesson on the overhead
and (very briefly) reviewing it. Discussion of the homework will follow.
The teacher will then move into a discussion on the hyperbola.
Students will be encouraged to develop their own definitions of a hyperbola.
The teacher will demonstrate the construction
of a hyperbola emphasizing the
properties of the hyperbola and its foci, vertices and asymptotes. This
discussion will be used to guide students toward discovering how a hyperbola
is constructed by the intersection of a double right circular cone and a
plane. Before this discussion, demonstrate how a hyperbola is formed using
a flashlight. Holding the flashlight against the wall will produce one half
of a hyperbola with focus being the light bulb of the flashlight.
In activity one, the students will use a model similar to the
one used in the previous lesson to discover that a hyperbola is formed when
a plane intersects both nappes ("halves") of a double right circular
cone but does not intersect the vertex of the cone. The teacher will provide
guidance to the groups as they construct their hyperbola and will clear
up any misconceptions or misunderstandings the students have concerning
the construction process. Once the constructions are complete, the teacher
will facilitate a discussion concerning these constructions and their relation
to the definition of a hyperbola. The students will then move on to exploring
the equation of a hyperbola.
Activity two will begin with the teacher explaining that the
standard equation for a hyperbola like that for the circle and ellipse is
derived from the distance formula. The teacher will present to the students
a given hyperbola centered at the origin and having given foci and vertices.
Students will use their definitions of a hyperbola along with the distance
formula to derive the standard equation for this given hyperbola. The teacher
will circulate checking for correctness and providing guidance. The students
will then generalize the equation to that of an arbitrary hyperbola with
arbitrary center, foci, vertices and a horizontal or vertical major axis.
In activity three, the students will work on several examples in
which they are either asked to determine the standard equation for a hyperbola
with given foci and vertices or to determine the foci and vertices given
the standard equation.
In activity four, the students will work on several examples in which they are either asked to determine the equation for a hyperbola with given foci and vertices or to determine the foci and vertices given the standard equation.
To end the discussion, the teacher will place the list of knowledge back on the overhead this time having the students add to that list the knowledge of hyperbolas they gained from this lesson. To assess the students progress, they will be asked to write in their journals about their knowledge of the hyperbola. As a minimum they should give their own definition of a hyperbola, describe how to obtain the equation of a hyperbola given its foci and vertices and explain why the general equation of a hyperbola is a special case of the general second degree quadratic equation Ax^2+Bxy+Cy^2+Dx+Ey+F=0.
To construct a hyperbola you will need 3 tacks, a ruler, a piece of string shorter than the length of the ruler, a pencil and a piece of board.
1. Tack the ruler to a piece of board so that it pivots at point A.
2. Tack one end of the string to the other end of the ruler, point B.
3. Tack the other end of the string to the board at point C. The distance between tacks A and C must be larger than the difference between the length of the ruler and the length of the string.
4. Holding the string taut against the ruler with a pencil, rotate the ruler about point A.
5. The resulting curve will be one branch of a hyperbola.
6. Repeat to get the other branch.

Activities:
Activity
1: Constructing a Hyperbola By
"Slicing" a Double Right Circular Cone
1. Flatten both nappes of your double right circular cone.
2. Find the line that is perpendicular to the axis of the cone and intersects the cone in a single point (i. e. the vertex of the double right circle cone). Select a point on this line.
3. Using your compass construct an arc
on the cone with this selected point as its center. Make sure this arc intersects
only one edge of each nappe of the flattened cone and does not intersect
the vertex of the cone.
4. Cut out the marked arc.
5. Open your cone back up and place the sheet of construction paper between
the two sections of the cone. Mark the intersection between the plane (i.
e. the construction paper) and the cone. What figure do you get? Is this
the only hyperbola that can be created by intersecting the cone with a plane?
6. What do you think would happen if the plane intersecting the cones was perpendicular to the base and intersected the vertex of the cone? This figure is called a degenerate hyperbola.
Activity
2: Deriving the Standard Equation
for a Hyperbola using the Distance Formula
Rotate roles before beginning this activity.
1. Determine the difference of the distances between the foci (point A and
point B) and the point on the hyperbola (point C) of the hyperbola below.
What will happen to this difference if you choose another point on the hyperbola?
Use the formula for the difference of the distances to determine the standard
equation of the hyperbola below.

2. Generalize the standard equation for an arbitrary hyperbola such as the one below. What would happen if the major axis of the hyperbola was the x-axis? What would happen if the center of the hyperbola was not located at the origin? Describe how the center, assymptotes and foci relate to this equation.
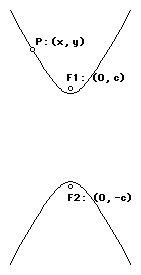
Activity
3: Determining the standard equation
of a hyperbola/ Determining the foci and vertices of a hyperbola
Rotate roles before beginning this activity.
1. Determine the standard equation and assymptotes for the hyperbola with
foci (0, 5) and (0, -3) and vertices (0, 4) and (0, -2).
2. Determine the standard equation and assymptotes for the hyperbola with
center at (3, 2) and foci at (6, 2), and (0, 2).
3. Determine the assymptotes, vertices and foci for the hyperbola with standard
equation x^2/9-y^2/4=1.
4. Determine the assymptotes, center and foci for the hyperbola with standard
equation y^/9-x^2/16=1.
Activity
4: Determining the general equation
of a hyperbola/Determining the assymptotes, vertices and foci of a hyperbola
with a general equation
Rotate roles before beginning this activity.
1. Determine the general equation for the hyperbolas in activity 3.
2. Determine the general equation and assymptotes for a hyperbola with foci
(4, 0) and (-1, 0) and vertices (2.5, 0) and (.5, 0).
3. Determine the assymptotes, foci and
vertices of the hyperbola with the general equation x^2-3y^2-4x+18y-50=0.
4. Determine the assymptotes, foci and vertices of the hyperbola with the
general equation 9y^2-5x^2+30x-36y-54=0.
5. Does the graph of every equation of the form Ax^2+Cy^2+Dx+Ey+F=0 determine a hyperbola? If yes, why? If no, give a counter example.
Assessment:
Journal Assignment: In your journal write about what you have learned
about the hyperbola. Give your own definition of a hyperbola, focus, vertex,
assymptote and center. Describe the construction of a hyperbola using a
plane and a double right circular cone (i. e. what is the mathematics behind
the construction we did in class?). Describe how to obtain the equation
of a hyperbola given its center and foci. Explain why the general equation
of a hyperbola is a special case of the general second degree (quadratic)
equation Ax2+Bxy+Cy2+Dx+Ey+F=0.
Did you know?
In grammar, the word hyperbole means "an exaggerated statement used specifically as a figure of speech for rhetorical effect". How do you think this meaning relates to the meaning of the word hyperbola in mathematics?
There are 70 known comets that have hyperbolic orbits with the sun being a focus.
A supersonic jet traveling parallel to the ground has a shock wave in the shape of a right cone. The sonic boom is felt on all the points located on the intersection of this cone and the ground. This intersection forms one branch of a hyperbola.
Since WWII, ships and planes have used the LORAN (LOng RAnge Navigation) system to determine their location. The LORAN system makes use of radio pulses that are broadcast at the same time from widely separated transmitters. The radio signals allow a ship or plane to locate itself at the intersection of hyperbolic curves.