
Exercise 2 asked me to cut a square from each corner of a 15by25 sheet of cardboard and fold along this cut line to from a lidless box. The diagrams below graph the volume function y = x(15 - 2x)(25 - 2x) in Algebra Expresser. The graph has been stretched to better show the maximum volume and sizes which have a volume of 400 cubic inches.

Maximum volume is attained when x = 3 of 513 cubic inches. Solving algebraically, volume is 400 cubic inches when x = 2/3 + 1/3sqrt13 and x = 2/3 - 1/3sqrt13.
The next solution will involve EXCEL.
| 1 | 13 | 23 | 299 |
| 1.25 | 12.5 | 22.5 | 351.5625 |
| 1.5 | 12 | 22 | 396 |
| 1.75 | 11.5 | 21.5 | 432.6875 |
| 2 | 11 | 21 | 462 |
| 2.25 | 10.5 | 20.5 | 484.3125 |
| 2.5 | 10 | 20 | 500 |
| 2.75 | 9.5 | 19.5 | 509.4375 |
| 3 | 9 | 19 | 513 |
| 3.25 | 8.5 | 18.5 | 511.0625 |
| 3.5 | 8 | 18 | 504 |
| 3.75 | 7.5 | 17.5 | 492.1875 |
| 4 | 7 | 17 | 476 |
| 4.25 | 6.5 | 16.5 | 455.8125 |
| 4.5 | 6 | 16 | 432 |
| 4.75 | 5.5 | 15.5 | 404.9375 |
| 5 | 5 | 15 | 375 |
| 5.25 | 4.5 | 14.5 | 342.5625 |
| 5.5 | 4 | 14 | 308 |
| 5.75 | 3.5 | 13.5 | 271.6875 |
| 6 | 3 | 13 | 234 |
| 6.25 | 2.5 | 12.5 | 195.3125 |
| 6.5 | 2 | 12 | 156 |
| 6.75 | 1.5 | 11.5 | 116.4375 |
| 7 | 1 | 11 | 77 |
| 7.25 | 0.5 | 10.5 | 38.0625 |
| 7.5 | 0 | 10 | 0 |
In the spreadsheet, I let the square side length vary in .25 increments from 1 to 7.5. When x >7.5, the side 15 - 2(side) would be negative which is not possible. Maximum value is again when side length of the square is 3 units. Volume is 400 cubic inches at approximately 1.6 and 4.6 units.
I will endeavor to show a solution with GSP if time permits.
1. A study of the graphs of the equation xy = ax + by + c, for various real number coefficients a,b, and c.
First, I will graph the function xy = 3x + 3y + c as c =-2,-1,0,1,2. This group of graphs appears below.
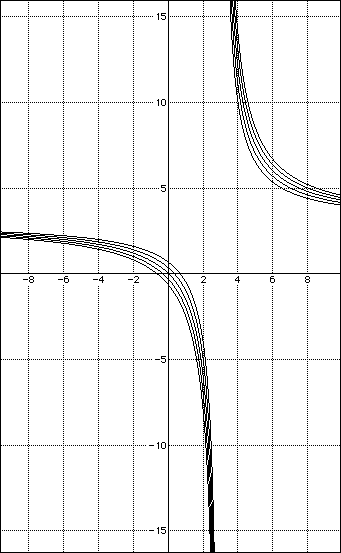
The next group show xy = 3x + by + 3 as b = -2,-1,0,1,2.
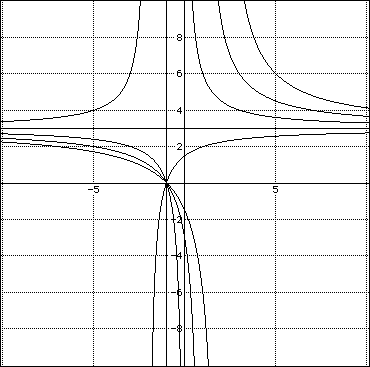
The last group show xy = ax + 3y + 3 as a = -2,-1,0,1,2.
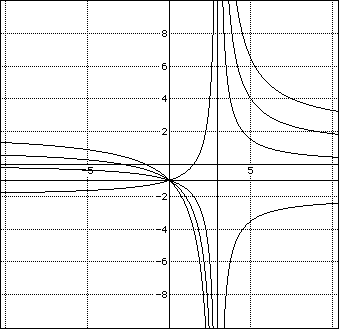
The graphs are all hyperbolas as long and a and b are non-zero. When a or b are zero, the graph represents the axis shifted. The values of a and b in general determine the assemptotes of the graphs. The function is going to reach limits for the function of c when the values of a vary and y approaches infinity, and the function approaches x = a as x approaches infinity. n As the values of b vary, the limits as x approaches infinity is c and asy approaches infinity is b. When c varies, the limit of the function as x and y approach infinity is a and b respectively. To prove this conjecture, here is another group of graphs with c varing and a> b.
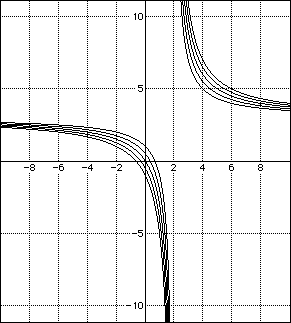 I used the equation 3x + 2y + c as c =-2,-1,0,1,2. The limit of x is
3 (a) and y is 2(b). The conclusion holds.
I used the equation 3x + 2y + c as c =-2,-1,0,1,2. The limit of x is
3 (a) and y is 2(b). The conclusion holds.
I analyzed the data by looking at the individual graphs. It would be easy to extend this with students by allowing a ,b,and c to have negative values.
For this write-up, I have selected the investigation of part a # 1 with negative value of a and b as c varies.
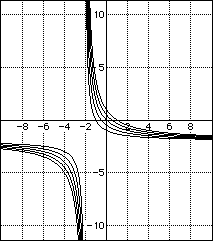
As expected for xy = -2x -2y + c, the limits have changed to -2 to reflect the new values of a and b.
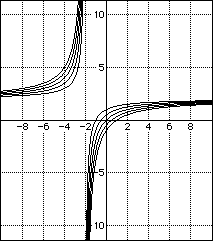
The graphs above is a slight variation of the form xy = 2x -2y + c. The limits of x have changed from -2 to 2 to reflect the change in the a value.
The unfinished exercises of assignment 9 probably represent my best work in the course. In completing the exercise, I was compelled to use the script I developed to draw a pedal triangle and also use the scripts from assignment 5 to create the varoius types of points to call the pedal point. For example, I used the incenter script to find a point and a triangle for the pedal triangle script to work from. I was learning to move from page to page to page as I used material from two pages to create diagrams for the page being created. It was extremely satisfying to be able to create 5 diagrams and save them in the final document in about 25 minutes. It was a very useful exercise to use with students to show the adaptation of documents to new applications. Even though the pedal script was ultimately for insertion in assignment 5, it was essential to the completion of assignment 9. I did not manage to get all the diagrams into assignment 9 on the first attempt, but the diagrams were all put into final page form. I am still relatively computer illiterate, but was very comfortable moving between the two pages to create and copy the diagrams.