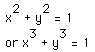
WRITE-UP 1

Assignment 1 involves the selection of one problem to write-up. I have selected problem 6 to write-up. Problem 6 involves the graphs of even and odd power functions of x and y always equal to 1. the end of the problem involves the expectation of what will occur with these functions when taken to the 24th and 25th powers. I would expect the even powers to be a closed curve, either circular or elliptical. The odd powers I expect to represent an 's' or 'w' in shape.

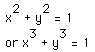
As expected, the graph of the square function became a circle, but the cubic function behaved in an unexpected manner.

The circular graph is the square equation, the other graph is the cubic function.



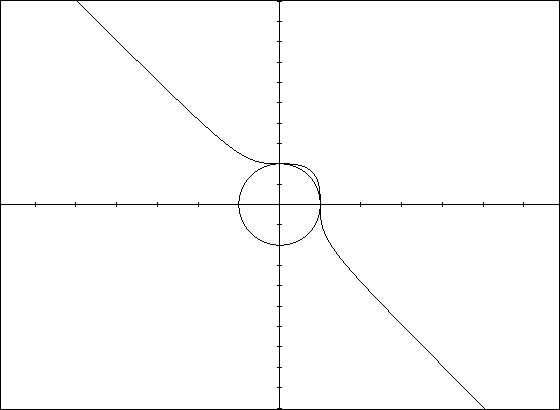
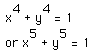
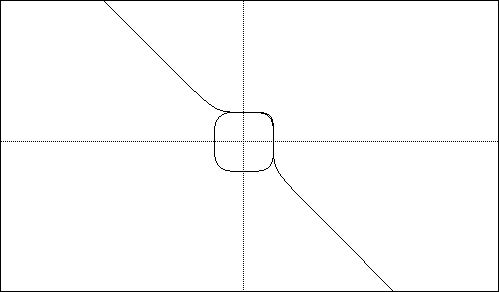
The 'round' graph in the middle is the quartic equation. The strange almost linear graph is the fifth degree function.


Slightly different results to what I expected. The even powers are going to get nearer and nearer to a square graph. The odd powers are going to become nearly linear in the intervals from -infinity to -1 and 1 to infinity. From -1 to 1 the graph will resemble a half square. When I graphed the 24th and 25th powers of these equations, the 24th power was square to the naked eye, and the 25th power resembled a half square from -1 to 1 and linear elsewhere. As the even powers become very large, the graph will become nearer to square. The graph can never become exactly square but will come close as the powers get very large.

Return