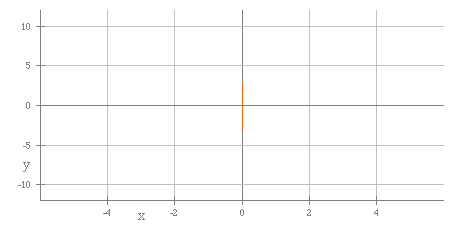
The first graph shows a = 0 and b = 3.
The second graph shows a = 0.25 and b = 3.
for values of t ranging from 0 to 360 degrees inclusive. Mathematically
this range is from 0 to 2pi, but I have never seen a computer that will
do the symbol for pi or the less than or equal and greater than or equal
symbols.
The first graph shows a = 0 and b = 3.

The second graph shows a = 0.25 and b = 3.
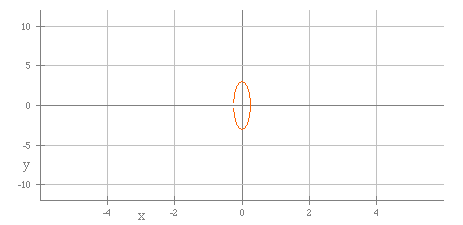
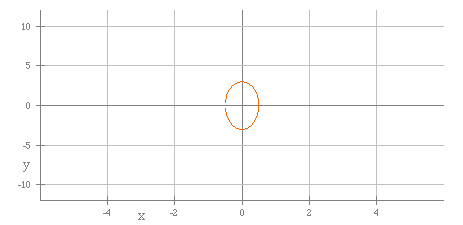
The next graph shows a = .5 and b = 3.
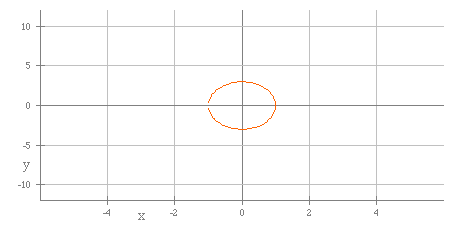
The next graph shows a = 1 and b = 3
The next graph shows a = 2 and b = 3.
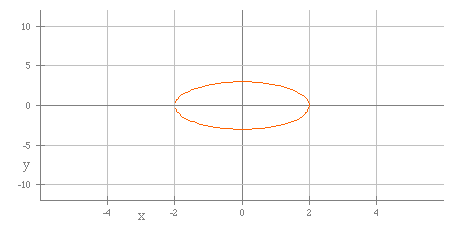
The next graph shows a = 3 and b = 3.
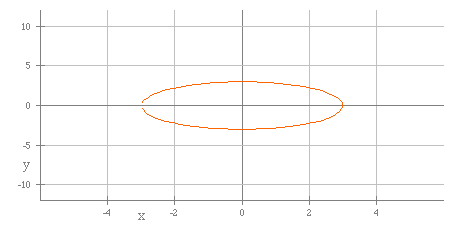
The next graph shows a = 4 and b = 3.
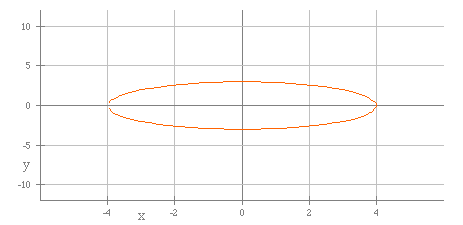
The next graph shows a = 5 and b = 3.
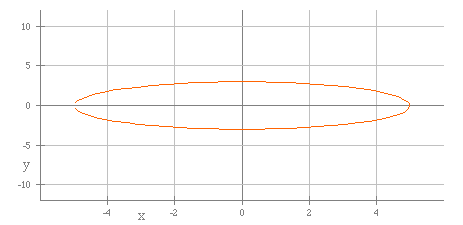
In terms of the t parameter, the graphs show basic eliptical tentencies,
with the values of a and b becoming the maximum and minimum distances along
each axis.
Now lets see if the same results hold when b is varied and a stays a constant
value.
The first graph shows a =3 and b = 0.
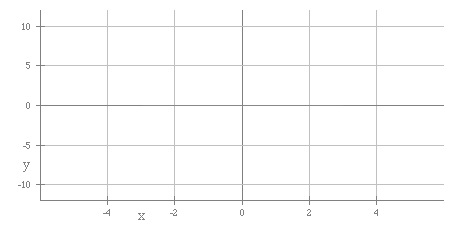
The next graph shows a = 3 and b = 0.25.
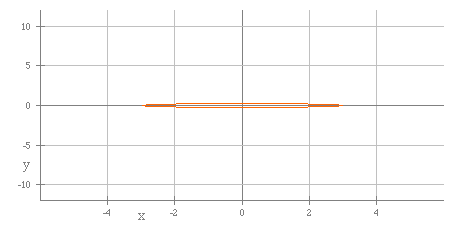
The next graph shows a = 3 and b = 0.5.
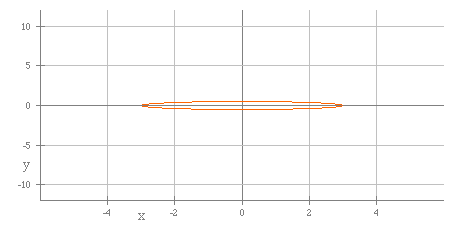
The next graph shows a = 3 and b = 1.
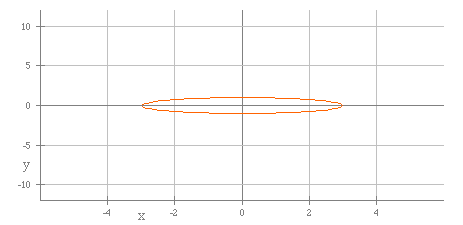
The next graph shows a = 3 and b = 2.
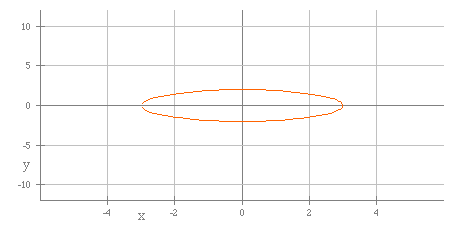
The next graph shows a = 3 and b = 3.
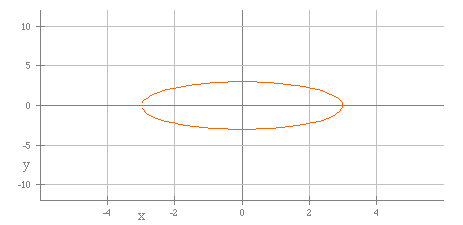
The next graph shows a = 3 and b = 4.
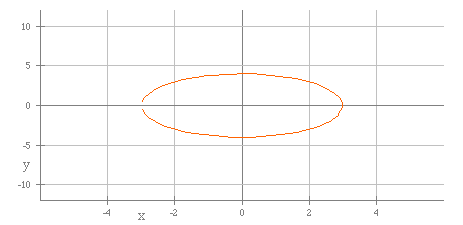
Lastly, the graph where a = 3 and b = 5.
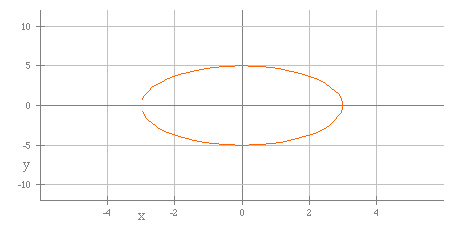
The preliminary premise seen after the a values were varied holds for
the graphs where b was varied. This makes logical sense when considering
the actual graphs of sin t and cos t. The maximum value is always determined
by the constant term in front of the function. The sine and cosine values
usually range from 1 to -1 as a matter of course. This exercise is valuable
for students to reinforce the concept of function limits and the manner
of change of these limits as the function varies from sin(t) to a sin(t)
to sin (at) to sin(t) +a , etc. A variety of different functions need to
be graphed to best reinforce the variations.