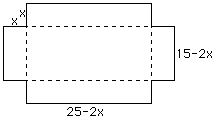
Herein will be discussed the solution to the following problem:
Given a rectangular sheet of cardboard 15 in. by 25 in., if a small square of the same size is cut from each corner and each side folded up along the cuts to form a lidless box,
a) What is the maximum volume of the box?
b) What size(s) of the square would produce a box of volume equal to 400 cubic inches?
Solution
The most common way to represent this problem is to call the length of the sides of the cut-out squares x--yielding a diagram such as this:
Thus, the equation for the volume of the resulting box (fold along the
dashed lines) is given by 
.
Given this setup, we can answer parts a) and b) in a variety of ways:
Using Algebra Xpresser, we can graph and "Xplore" it's
maximum values.
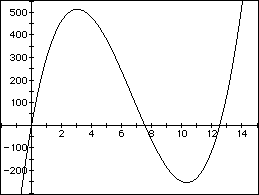
Since the y-axis represents the volume of a box, it doesn't make much
sense for y to be negative. Also, if x were bigger than 7.5 we would have
cut out more than we had to start with. Thus, we can limit our domain to
.
The graph appears to attain a maximum of a little more than 500 when x is about 2.5. It also appears to achieve the value of 400 when x is about 2 and again when x is about 4.5.
At this point we could turn to Calculus to give us exact answers, but let's see how much more information we can get from graphing.
For part a) let's zoom in and see what we can get:
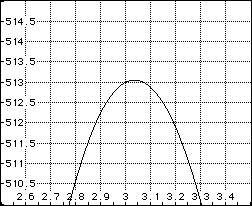
Not bad, the maximum volume of the box appears to be a tad more than 513 cubic inches.
In part b) we are looking for a solution to 
. Graphing this equation
shows two solutions in our given domain.
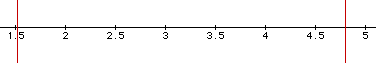
We can see that the solutions are pretty close to 1.5 and 4.75.
For the time being we have the following approximate answers.
a) a maximum volume of 513 cubic inches
b) a volume of 400 cubic inches when x=1.5 inches or x=4.75 inches.
(Note, 
-- so these aren't bad, they just aren't exact---yet)
Let's try using a spreadsheet to manipulate our volume function.
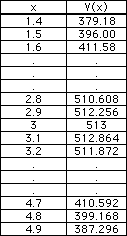
We can easily evaluate our volume function using a spreadsheet. Here we have the areas in which we were most interested. Our estimates from above our justified nicely.
Before we get our exact answers, let's see if we can get a little more accurate by narrowing down our inputs in the spreadsheet. This "guessing" method is quick and easy.
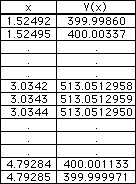
Well, as you can see, the results are quite nice. We now have the following as solutions:
a) The maximum volume, accurate to 5 decimal places, is 513.05129 cubic inches.
b) To attain a volume of 400 cubic inches, we can choose either of the following: x=1.5249 or x=4.7928 (accurate to 4 decimal places)
Of course, we could continue this process until we obtained whatever level of accuracy is desired/required.
As was mentioned above, we could resort to calculus to find these answers. However, notice how quickly the calculus method leads to "ugly" algebra.
We can maximize V(x) by finding the solution(s) to V'(x)=0. Now
,
so 
. We solve this using the quadratic formula and get the following two
values: 
. Only the smaller one falls in our domain.
Thus, the value of x which maximizes the volume is 
.
If we want an exact answer, we must evaluate V(x) for this x--which gets messy pretty fast. Plugging this in a calculator yields the same approximation as above.
Answering part b) is somewhat more difficult since we must solve the
cubic equation .
I hope you enjoyed exploring the solution to this problem. I know I did.