Assignment #6, Problem #3.
Triangles and Median Triangles.
by: Kelli Nipper
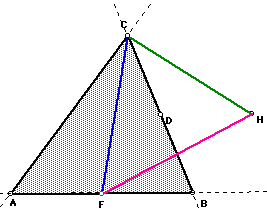
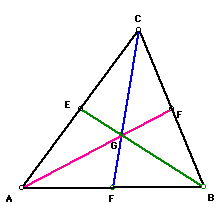
Our exploration begins with the construction of triangle
ABC and its medians AD, BE, and CF.
One method for creating the medain triangle is to use 2 of the medians as
radii of two circles with midpoints at the endpoints of the 3rd median.
The point of intersection is the 3rd point of the triangle.
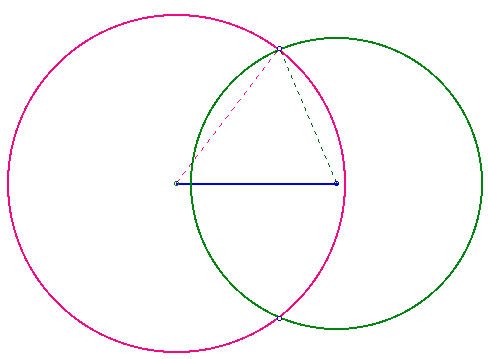
This figure can be used to reinforce the idea that the sum of the 2 sides
of the triangle must be greater than the hypotenuse
Another method for constructing the medians triangle is
more useful in finding relationships between the triangle ABC and its medians
triangle.
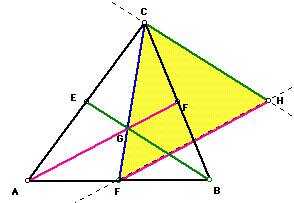
Construct a second triangle with the three sides having the lengths of the
three medians. Using line segment CF as the base of the new triangle, a
line parallel to AD through point F and a line parallel to BE through point
C can be constructed. We can see that a triangle is created by the intersection
of the parallel lines. The new triangle is the medians triangle.
Click Here to view the properties of median
triangles for various triangles.
In exploring various shapes for triangle ABC, I found:
- The point C is a vertex of both triangles.
- The centroid of the medians triangle (CHF) is the midpoint of BC in
the original triangle.
- The midpoint of AB is a vertex of the medians triangle.
Using these observations, I recreated the original triangle (given the
medians).
I constructed a line through points C and D. Using this line as the base
of the triangle, a line parallel to HK through point F, and a line parallel
to FJ through point C could be constructed.
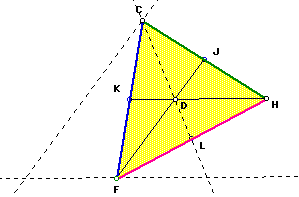
The new triangle is the original triangle with medians the length of the
sides of the medians triangle.