Assignment 7
Tangent Circles

by Kelli Nipper

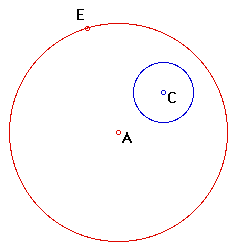
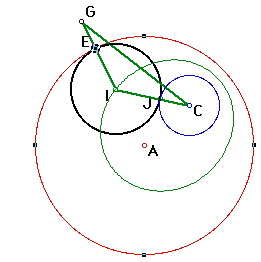
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

2. Construct a line through center A and point E. (The center of the tangent circle must lie on this line.)

3. Construct a circle with center E and radius equal to circle C. (This radius is EG)

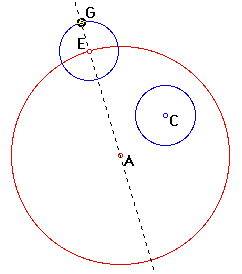
Since the center of the tangent circle must be equidistant from point E and circle C, then if we extend the segments by a distance equal to radius C, the center of the tangent circle must also be equidistant from point G and center C.

4. Connect point C and point G. (This will be the base of the isosceles triangle.)

5. Construct a perpendicular bisector through the midpoint of GC. The third vertex of the isosceles triangle is where the two constructed lines intersect. This point is also the center of the tangent circle.

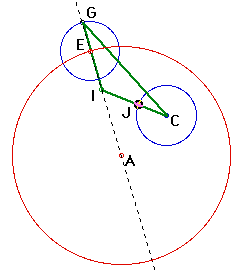
6. Construct a circle with center I and radius IE.

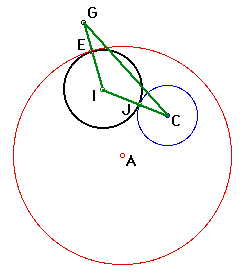
The foci are located at the centers of the given circles ( A and C ).--> The two sides of the isosceles triangle ( IG and IC ) are equal in length by definition. Therefore, the distance from center I to center C plus the distance from center I to center A is the same as the sum of the radius's of the given circles (A and C). This is the definition of the foci of an ellipse.

In closing, to extend this problem--Given two circles and a point on one of the circles, investigate the tangent circle if :

• the two circles are mutually exclusive
• the smaller circle is on the larger circle.
• the smaller circle is internal to the tangent circle.
• the point is on both circles.

Return to Kelli's Class Page