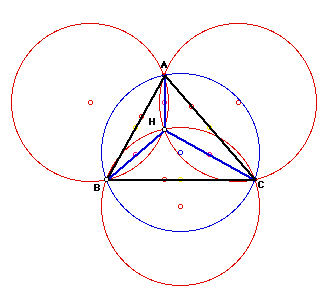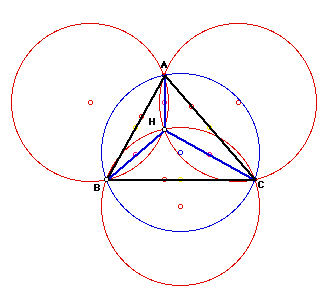Assignment 8
Altitudes and Orthocenters
by Kelli Nipper
After constructing the orthocenters for the four triangles, it was obvious
that for any triangle:
- Point A is the orthocenter for triangle HBC.
- Point B is the orthocenter for triangle HAC.
- Point C is the orthocenter for triangle HAB.
Click Here to view
the orthocenter's position for various triangles.
Next, I constructed the circumcircle for the four triangles.
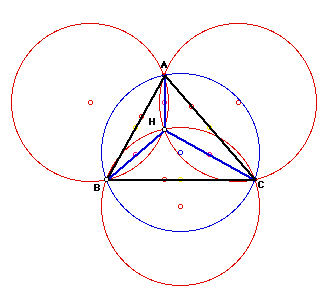
Connecting the centers of triangle HAB, HAC, and HBC creates a triangle
congruent to triangle ABC.
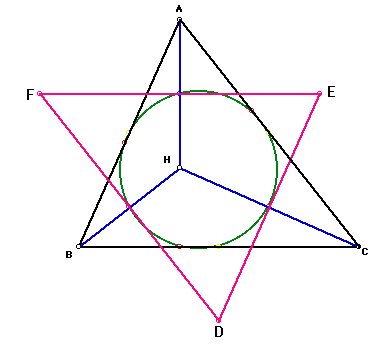
This is obvious since AB is congruent to DE; BC is congruent to EF; and
CA is congruent to DF. These triangles are translations of each other.
After constructing the nine-point circle for triangles ABC,
HAB, and HBC, I found that they were all the same circle. This is true because:
- The feet of the altitudes coincide with the orthocenter.
- The midpoint of the segments from respective vertices to the orthocenter
coincide with the midpoints of sides and vice versa.
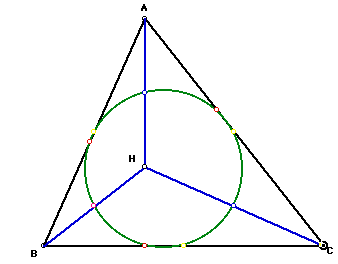
I found that the midpoints of the sides of triangle ABC(Yellow) are the
same as the midpoints of the segments connecting the vertices of the orthocenter
(Point C) of triangle HAB. (and vice versa giving us 6 of the 9 mandatory
points. The final 3 points(Red) come from the feet of the altitudes which
coincide for the 4 triangles.
Return to Kelli's Class Page