Dear Picky Nicky,

I wanted to tell you about this cool activity I did in school this summer. I know that Geometry is your favorite, and I really think you will enjoy this exploration.

I was assigned to start constructing triangles on a grid. On this grid, the horizontal or vertical distance between two dots represents a unit. The area of one square formed by connecting four dots with four one unit sides is a square unit.

To help you understand the investigation, you need to know a few terms. In the figure below, points A, B, C, D, E, F, G, H, I are called boundary points or "B". Point Z is called an interior point or "I".

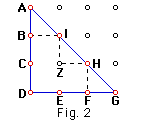
Area = 4.5 units2

There are several methods to calculate the area of figure 2. You can count up the number of whole squares and then add the number of half squares. Or, using the formula for the area of a triangle, you can multiply the base times the height and then divide by two. Remember, the height is the perpendicular distance from the base to the opposite vertices. (In obtuse triangles, the height is outside of the triangle.)

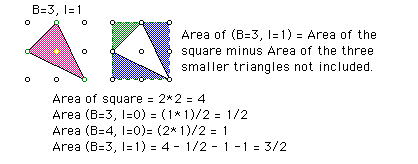
Sometimes, you don't have enough information to use either of these methods. To calculate the area, you can use a subtractive method. The subtractive method involves finding a known area that encompasses the smaller desired area and subtracting out the areas not included.

For example:

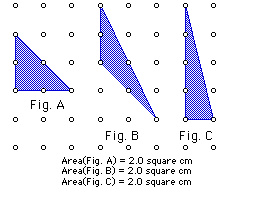
My first realization was that no matter what shape the triangle is, if it has a set number of boundary points and a set number of interior points, than the area of the figure will be the same. The following diagram illustrates this finding for 3 different figures with B=6 and I=0.

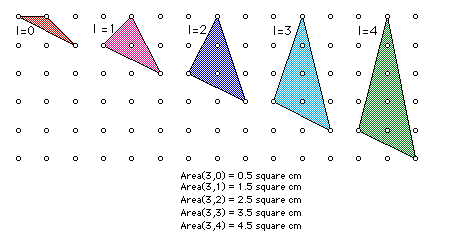
I first focused on exploring how the area changed keeping the number of boundary points constant at 3 and increasing the number of interior points by increments of 1.

The following figures have identical areas even though they have different shapes. This supports my first conclusion that if any two figures have corresponding border and interior points, than there areas will be equal.

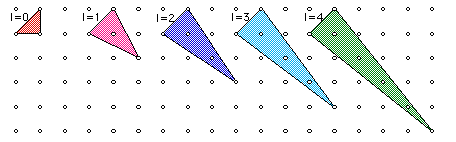
Using these figures, I began a chart that looks like the following:

From this chart, you can easily see that the area of a triangle with 3 boundary points is .5 square units more than the number of interior points.
ie. Area when B=3 is I + .5 or I + 1/2

Changing gears, the next step was to explore how the area of the triangle changed when the number of interior points remained constant at 0.

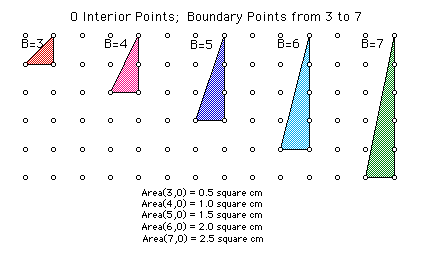
I made the following chart:

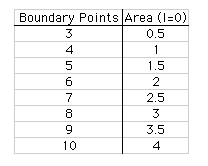
This pattern is not as easy to see. However, the area of a triangle with zero interior points is half of two less than the number of boundary points.
ie: Area when I=0 is .5(B-2) or (B-2)/2

So, if there are 3 border points, as you increase the interior points by 1, the area increases by 1. For 0 interior points, as you increase the border points by 1, the area increases by .5.

Putting the two charts together and continuing the sequence:

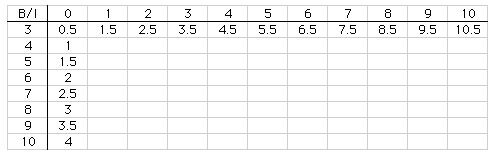
I predicted that these patterns would continue for the remaining entries. An investigation of a few random triangles with different numbers of interior and border points, yielded the following areas:

Plotting the new areas:

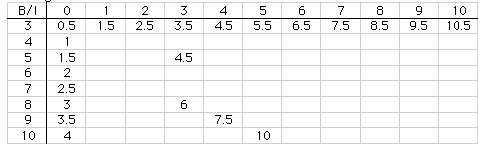
This is enough data to see that our prediction is true and we can fill in all of the remaining areas. I have provided a grid for you, Picky Nicky, so you can check that this is accurate.

I hope that you have enjoyed the exploration so far. At this point you are probably saying, "but, isn't there an easier way?" And you would be right to ask. For large triangles, filling in the chart or even trying to represent it on a grid, would be very tedious. So, we can look at the patterns developed in the chart to help derive a formula that can be used for any triangle.
Let's start with one of the random figures we just investigated. Since we know that a figure with 3 boundary points and no interior points(3,0) is always going to have an area of .5, then we can relate any other figure to this one. For example, the randomly chosen figure (8,3). We know from our original investigation that the area of this figure can be expressed as: Area(8,3)=6. Keep in mind that our goal will be to relate this back to our original figure with A(3,0)=.5.

This is easiest to do by looking at a simplified version of our chart:

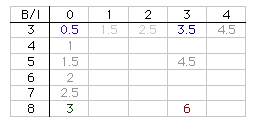
Remember: as you increase the interior points by 1, the area increases by 1, and as you increase the border points by 1, the area increases by .5

In order to go from Area(8,3) to Area(3,0), we must either move up the chart 5 steps to Area(3,3) and then left 3 steps to Area(3,0) or we can move left first to Area(8,0) and then move up 5 steps to Area(3,0).

Method 1:
Area(8,3)=Area(3,3) + .5 * 5 (for moving up 5 border points)
Since, Area(3,3)=Area(3,0) + 1*3(for moving left 3 interior points)
Area(8,3)=Area(3,0) + .5 * 5 + 1 * 3 (for moving up 5 and left 3 points)

So, Area(8,3)= .5 + 2.5 + 3 = 6

Method 2:
Area(8,3)=Area(8,0) + 1 * 3 (for moving left 3 interior points)
Since, Area(8,3)=Area(8,0) + .5 *5 (for moving up 5 border points)
Area(8,3)=Area(3,0) + 1 + 3 + .5 * 5 (for moving left 3 up 5 points)

So, Area(8,3)=.5 + 3 + 2.5 = 6

Generalizing this, the area of any figure with border points "B" and interior points "I":

Method 1: Area(B,I)=A(3,0) + .5 * (B-3) + 1 * (I)
Method 2: Area(B,I)=A(3,0) + 1 * (I) + .5 * (B-3)

Simplifying we see that Area(B,I)=.5 + .5B - 1.5 + I
=-.5B - 1 + I
=B-2 + I
2

This formula for calculating the area of a triangle by using the number of border points and interior points is called Pick's Theorem. Surprisingly, this formula is much more useful than we can even tell from this exploration.

Click here for a Mathematical Extension

Click here for a Pedagogical Extension

Return to Kelli's homepage