Area Mathematical Extension
by: Kelli Nipper

"Shearing with Geoboards"

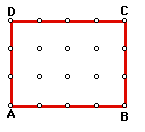
Construct any rectangle ABCD.

We see that we can calculate the area, which is the measure of how many square units there are in the two-dimensional figure, by counting the number of squares inside the figure.

Keeping the bottom base constant, move the top base one unit to the right.

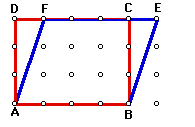
Calculating the area of ABEF, results in the same area as ABCD. This area conservation can be seen by shifting the triangle ADF perpendicularly from point A to point B. ADF is congruent to BCE, and ABCF remains the same. So, the area is equal.

This method of keeping the same base and shifting the top base(or points) in a direction parallel to the base and the same distance from the base, preserves area. The same is true with triangles.

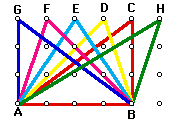
Figures formed by shearing have the same base and equal heights, and thus have equal areas.

Return to Pick's Theorem