

The two fundamental objects in geometry are points and lines. Even though we claim a certain amount of familiarity with these objects, we find it difficult to describe them due to their undefined nature. "It might be well to expand on what is meant by undefined. We do not mean that any word that is undefined is understood by everyone, or that everyone will attach the same meaning to the word. Essentially, we mean that such a word is uninterpreted. In various situations different interpretations can be given to the undefined word. For example, "line" may be interpreted as a pencil mark drawn along the edge of a ruler, as a line of sight for a surveyor, as a string held tight between two people. What we are trying to do in these examples is to point out that "line" in a given context has a meaning, or interpretation, associated with it"(Geometry:a perspective view, 4). It is a bit like trying to describe the taste of salt, we aren't quite sure how to describe it and to each person it might taste a little different. How would you describe a point? A point has no length, width, or thickness and we often use a dot to represent it. Points are labeled with capital letters, such as P.
A line is a straight arrangement of points.
There are more ![]() points on a line than anyone can count. It has no thickness
but its length goes on forever in two directions. Picture a telephone wire,
but a line is thinner, longer, and straighter than any wire ever made. The
animation to the right shows one way to think of the definition of a line
(line segment), as an
points on a line than anyone can count. It has no thickness
but its length goes on forever in two directions. Picture a telephone wire,
but a line is thinner, longer, and straighter than any wire ever made. The
animation to the right shows one way to think of the definition of a line
(line segment), as an 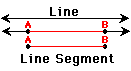 infinite number
of points.
infinite number
of points.
Parts of lines are called line segments. They are made up of two points and all the points on the line
between them. The two points are called endpoints and are named by capital letters
just like other points. It can also be named by a symbol like![]() .
.
A ray begins at a point and goes off ![]() forever
in one direction. A model of a ray is a laser beam. Two letters are needed
to name a ray; one is the point where it begins and the other is any point
it goes through. The symbol is the two letters with an arrow on top. Notice
that ray AB is not the same as ray BA.
forever
in one direction. A model of a ray is a laser beam. Two letters are needed
to name a ray; one is the point where it begins and the other is any point
it goes through. The symbol is the two letters with an arrow on top. Notice
that ray AB is not the same as ray BA.
An angle is formed by two rays which begin at
the same point (if the rays do not lie on the same line). The rays are called
the sides of the angle; the point of meeting is called the vertex. There are several
ways of naming angles: a capital letter at its vertex; a small letter within
the 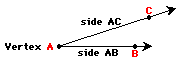 angle; a number within the
angle, or by three capital letters, the middle letter is the vertex , the
other two are points on each ray. We will name angles by the latter approach,
thus the angle to the right would be referred to as CAB or BAC. It is very
important that the middle letter always refers to the vertex of the angle.
angle; a number within the
angle, or by three capital letters, the middle letter is the vertex , the
other two are points on each ray. We will name angles by the latter approach,
thus the angle to the right would be referred to as CAB or BAC. It is very
important that the middle letter always refers to the vertex of the angle.
Acute, Right, Obtuse, Straight, and Reflex
Adjacent, Vertical, Congruent, Complementary, and Supplementary
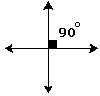
Perpendicular
Lines
Perpendicular lines
(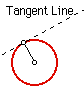 but in science and engineering. Graphs in either two
or three dimensions have axes at right angles to each other. Gravity acts
perpendicularly to the horizontal. The tangent of a circle is perpendicular
to its radius. In buildings walls must be perpendicular to floors. How many
other perpendicular relationships can you find? but in science and engineering. Graphs in either two
or three dimensions have axes at right angles to each other. Gravity acts
perpendicularly to the horizontal. The tangent of a circle is perpendicular
to its radius. In buildings walls must be perpendicular to floors. How many
other perpendicular relationships can you find? |
 |
Parallel lines (| |) are lines that lie in the same plane but do not intersect. That is, if they are extended indefinitely, they will never meet. This means that they must be the same distance apart. To say line n is parallel to line m, we write n | | m. In the Olympics, some gymnastic events are parallel bars and uneven parallel bars. Men and women gymnasts are judged on required moves and difficulty in their routines. |
 |
Point, Line and Angle Experiments