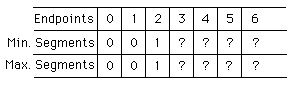
While searching through a textbook for interesting explorations
for middle school students I came across the below chart. At first glance
it seemed to be simply a fill in the blank no thinking exercise but as
I investigated it a little further, a number of interesting patterns emerged.

Rules for creating and counting
line segments.
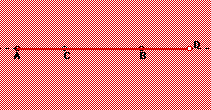
In creating segments, do not cross
another segment.![]() For
example, the red line is not to be
used. If you can connect two points with a line segment, you must do so.
In counting segments,
do not double count overlapping segments.
For
example, the red line is not to be
used. If you can connect two points with a line segment, you must do so.
In counting segments,
do not double count overlapping segments. ![]() This
picture represents two line segments, not three.
This
picture represents two line segments, not three.
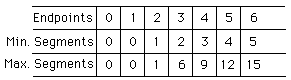
First Pattern - Minimum Segments
Obviously, when two points are provided the minimum number
of segments that can be formed is one. When a new point is introduced,
we have two choices as to where to place the point; on the line segment
(or its extension) or off of the line. We find that by placing the point
on the line segment or on its linear extension only one more line segment
is formed, which is obviously still a minimum. This pattern continues on.
Thus the process for creating a minimum number of segments is to create
collinear points. A formula that you could use for calculating the minimum
number of segments is minimum segments = (# of points) - 1
![]()
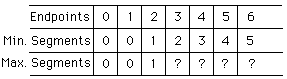
Second Pattern - Plane Division
Is it possible to represent all segment values between
the minimum and maximum? This is a easier question to answer, then it is
to prove. After a little investigation, I came to find that by dividing
the plane into regions I was able to show which situations were possible.
Thus enabling me to determine an answer to the above question.
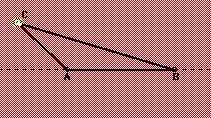
THREE POINTS IN THE PLANE
Two points already on the plane, and we are placing the third point.
As mentioned earlier two points create only one possible situation: one line segment. When we look for possible place for the third point we find that the plane gives us two possible locations.
 |
(Left) Given two points we find two possible
regions to place the third point. Region #1(Red)
Anywhere off of the line or its extension. Region #2 (Black) The
line or its extension.
(Left Down) When we place the third point off of the line we notice the formation of two new segments giving us a total of three line segments for three points. (Down) When the third point is placed on the line or its extension we notice that only one new line segment is created, giving us a total of two line segments for three points. |
 |
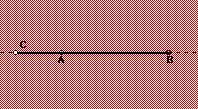 |
Summary for three points - In this case the minimum is two while the maximum is three. Obviously we can represent all segment values between the minimum and the maximum because in this case there are no segment values between them.
|
|
|
| MINIMUM (2 segments) | |
| MAXIMUM (3 segments) | |
FOUR POINTS IN THE PLANE
When working with four points we have two possible arrangements
to begin with. The case where 2 segments are formed by 3 points and the
case where 3 segments are formed by 3 points.
CASE #1 -Working from the minimum arrangement![]()
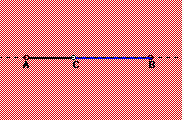 |
(Left) Given three points(minimum arrangement)
we find two possible regions to place the third point. Region #1(Red) Anywhere
off of the line or its extension. Region #2 (Black & Blue) The line
or its extension.
(Left Down) When we place the fourth point off of the line we notice the formation of three new segments giving us a total of five line segments for four points. (Down) When the fourth point is placed on the line or its extension we notice that only one new line segment is created, giving us a total of three line segments for four points. |
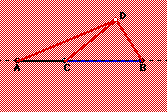 |
 |
Summary of Case #1 - Thus two possible values exist when we begin with the minimum arrangement for three points. One formation of 3 segments and another of 5 segments.
CASE #2 -Working from the maximum arrangement![]()
(Right) Given 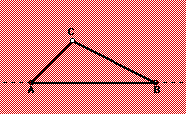 the
three points in their maximum arrangement(a triangle), we look for some
insight on where to place our next point.... inside.... outside.....??
the
three points in their maximum arrangement(a triangle), we look for some
insight on where to place our next point.... inside.... outside.....??
(Down) When working with this arrangement we find
that two regions are created in the entire plane. Region #1 (Yellow)
This region represents all points that are visible by the three vertices
of the triangle. Three segments are formed from the vertices to this new
point in region #1. Region #2 (Black & Green)
This region has two sub-regions: the black region includes placing
the new point on the sides of the triangle or their extension while the
green region represents the shadowed
regions where only two vertices are visible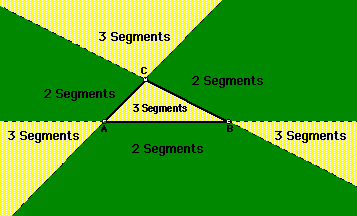 .
Placing a point in these regions creates two new segments. Region #1 and
Region #2 represent the entire plane.
.
Placing a point in these regions creates two new segments. Region #1 and
Region #2 represent the entire plane.
Summary of Case #2 -Thus two possible values exist when we begin with the minimum arrangement for four points. One formation of 3 segments and another of 5 segments.
Summary for four points - In this case we saw a number of possible arrangements, 3 segments, 5 segments and 6 segments. Our original question was whether we could represent all possible segment values from the minimum to the maximum. Well here is a case where we can say that it is impossible to create a four segment arrangement with four points. We know it is impossible because we have represented every point in the plane and at no location can only four segments exist.
|
|
|
| MINIMUM (3 segments) |
|
| MIDDLE (5 segments) |
 |
| MAXIMUM (6 segments) |
 |
Generalization for n points - To determine all
possible formations follow the below steps:
1) Take the previous points arrangements (Minimum, Middle(s)
and Maximum) and create a planar division display all possible point locations.
2) Determine the minimum, and the maximum segment values.
The minimum is created by placing the new point on the line segment of
the previous example minimum arrangement(see First Pattern - Minimum Segments).
The maximum is created by placing the point in a three segment region of
the previous examples maximum arrangement(see Third Pattern - Maximum Segments).
3) Determine the middle segment values. Create the regions
for the previous examples middle arrangements. These will display all possible
different combinations.
Third Pattern -Maximum Segments
Plane division helps us look at the pattern formed by
the maximum segments. We see that we can form the maximum segments when
we work off of the previous arrangements maximum formation. It is also
a fairly direct step to see that the maximum is three more than the previous
arrangements maximum. A formula that you could use for calculating the
maximum segments = 3 * ((# of points) - 1)

Fourth Pattern - Number of Segments to the Number of Triangles Formed
A nice pattern exists but I will leave this to be explored by the reader.
Further Investigation: How would things be different if we could cross segments? How would our maximums and minimums be effected if we could count overlapping segments?...... Altering the original parameters would quite drastically change the above observations..... explore.. and find out more.....