In today's classrooms, teachers are searching for various means to explore geometry. Usually you spend valuable class time drawing simple constructions, trying to illustrate new concepts. Using drawing programs like The Geometer's Sketchpad, students can explore new concepts easily and also understand different relationships between sizes or shapes.

 

During this write-up, we will explore the centroid of a triangle. The centroid is the common intersection of the three medians. A median of a triangle is the segement from a vertex to the midpoint of the opposite side. I will walk you step by step to construct the centroid using GSP. The first step is to construct a triangle by drawing a three segments that a joined at the endpoints. The triangle looks like the following:

 

Now name the vertices A, B, and C. We have triangle ABC below.

  

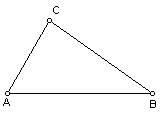
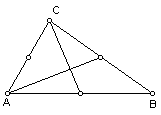
The next step in constructing a centroid is to find the midpoint of each segment (AB, BC, and AC). The midpoint of all three segments are shown below.

 

 

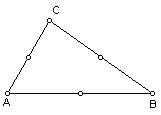
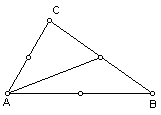
The third step is to construct the medians of the triangle. Recall, the median is the segment from a vertex to the midpoint of the opposite side.



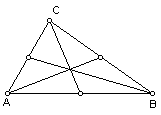
The point where all three medians intersect is called the centroid of the triangle ABC. Label the centroid G.

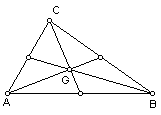
 Now that we have constructed the centroid of the triangle ABC, let's explore the location of G for different shapes of the triangle. Let's start our exploration by looking at an equilateral triangle.

 

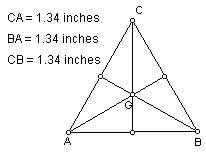
 Notice where the centroid is located. The centroid is located on the perpendicular bisector for all three sides of the triangle. How do you think an isosceles triangle and scalene triangle will differ?

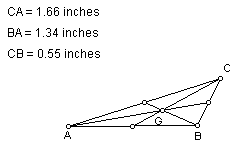
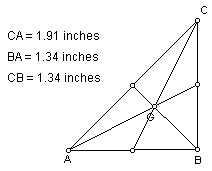
The centroid of course remains inside, but the centroid moves depending upon the triangle. On the isosceles triangle, the centroid lies on the perpendicular bisector of segment AB. However, centroid is not located on any perpendicular line or bisector.



Return to Kelly Pierce's Home Page