
The Department of Mathematics Education

and to overlay several graphs of
for different values of a, b, or c as the other two are held constant.
From these graphs discussion of the patterns for the roots of
can be followed. For example, if we set
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following
picture is obtained.
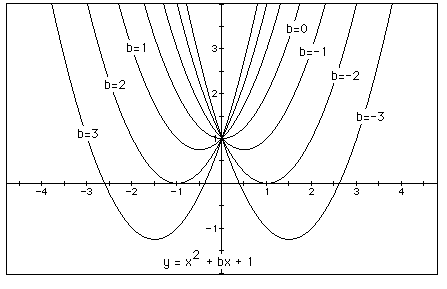
We can discuss the "movement" of a parabola as b is changed.
The parabola always passes through the same point on the y-axis ( the point
(0,1) with this equation). For b < -2 the parabola will intersect the
x-axis in two points with positive x values (i.e. the original equation
will have two real roots, both positive). For b = -2, the parabola is tangent
to the x-axis and so the original equation has one real and positive root
at the point of tangency. For -1 < b < 2, the parabola does not intersect
the x-axis -- the original equation has no real roots. Similarly for b =
2 the parabola is tangent to the x-axis (one real negative root) and for
b > 2, the parabola intersets the x-axis twice to show two negative real
roots for each b.
Now consider the locus of the vertices of the set of parabolas graphed from
The vertex of a parabola can be found by taking the derivative of the
equation and setting the equation equal to zero (this is actually finding
the maximum and minimum of the graph). This will give you the x-coordinate
of the vertex. The following is the equations:
If you check the coordinates of the vertices, you will see they satisfy
the equation y = - x^2 + 1 . However, I would still like to check small
values of "b" like "b" = 1/2 and 1/4. The vertices of
the 2 graphs also satisfy the equation y = -x^2 + 1.
Now, lets graph y = -x^2 + 1 on the same set of axes as above.
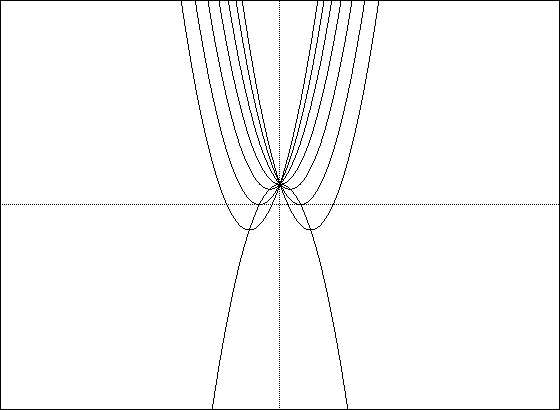
Look at the graph of ![]() . It can easily be seen that
the graph goes through all the vertices of y = x^2 + bx +1.
. It can easily be seen that
the graph goes through all the vertices of y = x^2 + bx +1.
Let's try the same for the graph of y = x^2 +bx +2 and see if the same applies
for
y = -x^2+2
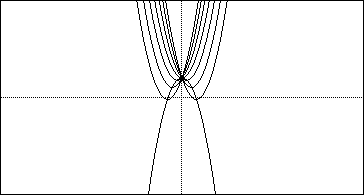
How did the graph change? The first major change seems to be the intersectin
point for all the graphs. The intersection points for the original graph
of y = x^2 +bx+1 was (0,1) and now the point has moved to (0,2). Lets analyze
that for a second. We changed the c value from "1" to "2"
and the intersection point changed accordingly. The move of the intersection
poin is logical since
y = x^2+bx+1 and y = x^2 +bx + 2 evaluated for x=0 is 1 and 2 respectivly.
To generalize, the vertices form the equation y = -x^2 +c from the original
equation y = x^2 +bx +c.
Consider again the equation
for b = -3, -2, -1, 0, 1, 2, 3 and overlay the graphs on the same set
of axes. The following graph is obtained.
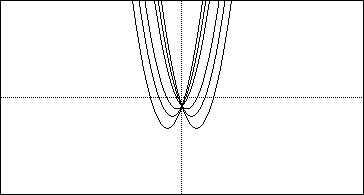
How does the y = x^2 +bx -1 graph differ from the y = x^2 +bx +1 graph?
First, you can tell the shapes of the graphs have remained the same. However,
the point where all the graphs intersect has moved from (0,1) to (0, -1).
From all the different values of "b" graphed are there any generalizations
that can be made?
Consider the equation y = x^2 +x +1 and y =- x^2 +x+1
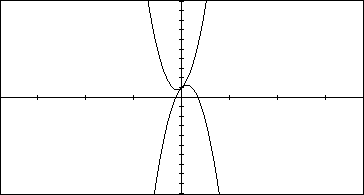
Notice, both graphs have the same shape and the only difference seems
to be one is concave up while the other is concave down.
What would happen if I changed the value of "a" to = 1/2 or 2.
Lets look at the graphs on the same set of axes.
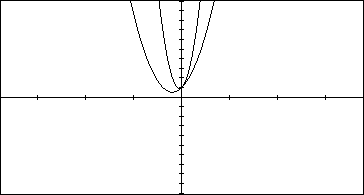
Some generalizations can be made. If a= 1/2 , the parabola is shrunk
vertically(made fatter). If a= 2, the parabola is stretched vertically (smaller).
Let's generalize the affects of "a" on the equation y = ax^2 +
bx +c. First, positive values of "a" opens the parabola upward
and negative values opens the prabola downward. The larger the values of
"a" (|a| .1), then the parabola opening becomes narrower. If the
|a| is between 0 and 1, then the parabola's opening will become wider.
Now graph this relation in the xb plane. We get the following graph.
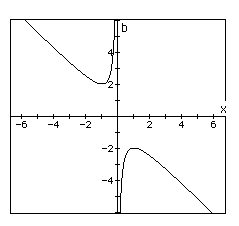
If we take any particular value of b, say b = 3, and overlay this equation
on the graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the roots of
the original equation for that value of b. We have the following graph.
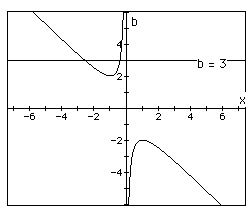
For each value of b we select, we get a horizontal line. It is clear
on a single graph that we get two negative real roots of the original equation
when b > 2, one negative real root when b = 2, no real roots for -2 <
b < 2, One positive real root when b = -2, and two positive real roots
when b < -2.
Consider the case when c = - 1 rather than + 1.
In the following example the equation
is considered. If the equation is graphed in the xc plane, it is easy
to see that the curve will be a parabola. For each value of c considered,
its graph will be a line crossing the parabola in 0, 1, or 2 points -- the
intersections being at the roots of the orignal equation at that value of
c. In the graph, the graph of c = 1 is shown. The equation
will have two negative roots -- approximately -0.2 and -4.8.
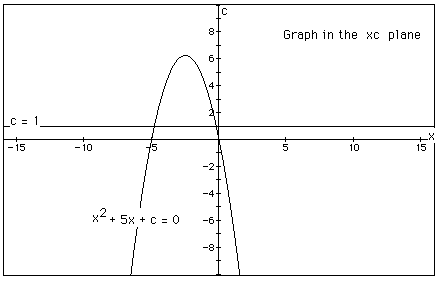
There is one value of c where the equation will have only 1 real root
-- at c = 6.25. For c > 6.25 the equation will have no real roots and
for c < 6.25 the equation will have two roots, both negative for 0 <
c < 6.25, one negative and one 0 when c = 0 and one negative and one
positive when c < 0.