The orthocenter (H) of a triangle is the common intersection of the three
lines containing the altitudes. You might ask, what is an altitude? An altitude
is a perpendicular segment from a vertex to the line of the opposite side.
Sometimes the segment does not intersect in the interior of the triangle,
it may be on the extension of the triangle. To construct the orthocenter,
you must first construct a triangle and name it ABC:

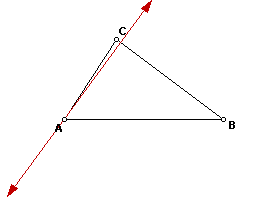
After constructing the triangle, construct the orthocenter by drawing the
perpendicular line from a vertex to the opposite side. The steps are as
follows:
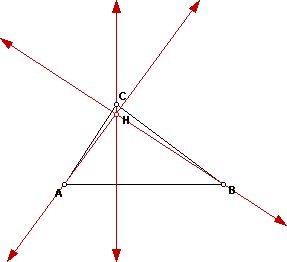
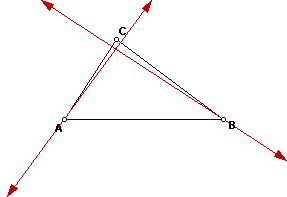
Now, I have constructed the orthocenter (H) for my triangle ABC.
The orthocenter will move as the shape of triangle ABC changes. The point
H will move outside the triangle when triangle ABC is a obtuse triangle
and the point H will be on the vertex if the triangle is 90 degrees.
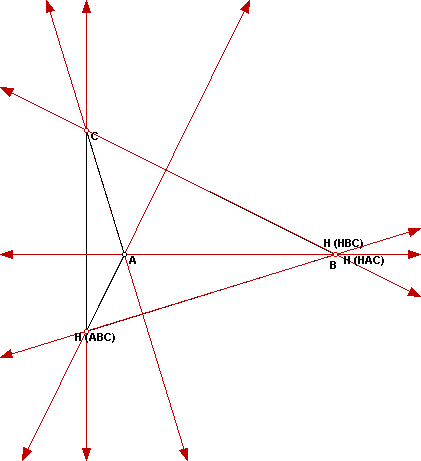
The next construction is to make the orthocenter of triangle HAB and it
looks like the following:
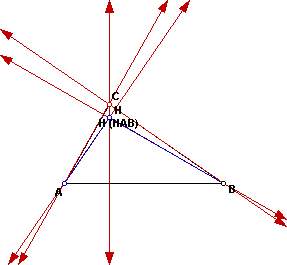
To continue, construct the orthocenter for triangle HBC and HAC.
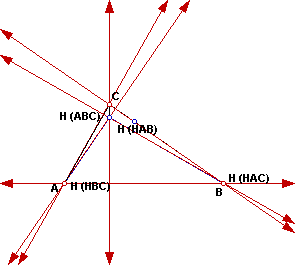
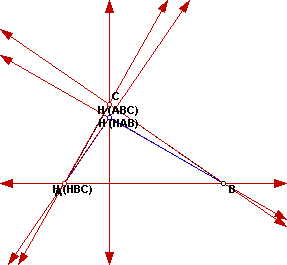
Look at the location of the orthocenters for the new triangles. The orthocenter
for triangle HAB lies on the segment BC. I found something interesting about
the orthocenter for triangles HAC and HBC. Both orthocenters lie on the
opposite vertex for the original triangle. (Orthocenter H (HBC) lies on
the vertex A and Orthocenter H (HAC) lies on the vertex B) Constructing
orthocenters are easy to do if you use the tool "script" in the
GSP software package. Otherwise you waste time reconstructing the same types
of lines and you can spend more time exploring. I was curious to see what
would happen to the different othrocenters if I changed the shape of triangle
ABC. Let's Explore!!
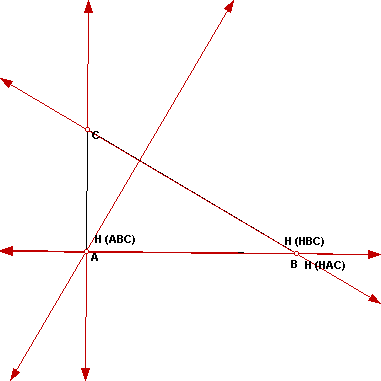
When triangle ABC is a right triangle, the orthocenters for HBC and
HAC are at vertex B, while H(ABC) lies at vertex A. However, when triangle
ABC is an obtuse triangle, the orthocenters for HBC and HAC lie at vertex
B, but H (ABC) lies outside the original triangle ABC.
Next, we will investigate circumcirles . Let's first construct triangle
ABC and the circumcircle for it.
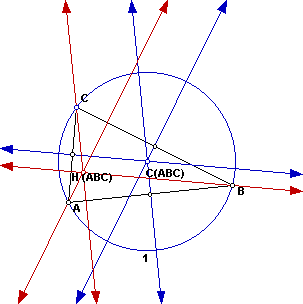
The triangle now has the orthocenter labeled H (ABC) and the circumcirlce
C(ABC). We used a script from our personal library to make the circumcirlce.
Now let's construct the circumcircle for triangle HBC, HAC, and HAB.
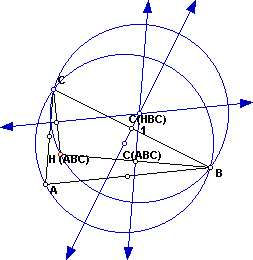
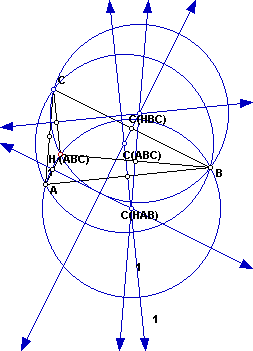
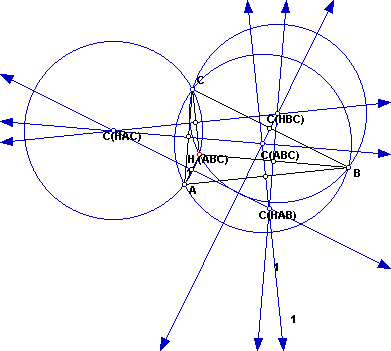
Look at the different Circumcenters and their locations. Let's expolore
how they move as the shape of ABC changes.
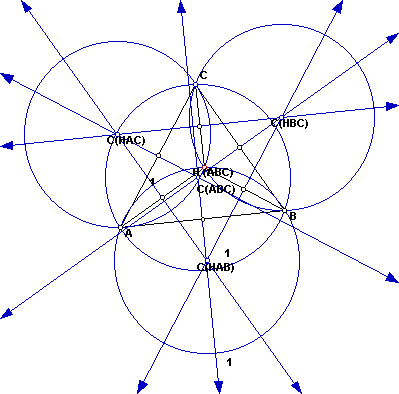
The shape of triangle ABC changed to an equilateral triangle and the circumcenter
of all the triangles relating to the orthocenter lie outside the triangle.
The radius of all the circumcenters are the same. Look at the triangle
that is made up of C(HAB), C(HAC), and C(HBC). This triangle has the same
perimeter as the original triangle ABC. Also, some pedals has been constructed
with the circumcenter. Now I would like to look at some special triangles.
First, construct a right triangle. What do you think would happen to the
constructions?
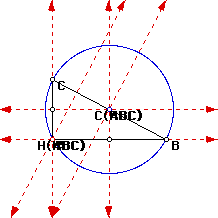
All the circumcenters of triangles ABC, HBC, HAB, and HAC lie on the
same point and therefore the circles are all the same. In addition, the
orthocenters of triangles ABC, HBC, HAB, and HAC all lie on the vertex A
of the original triangle. We can make the conclusion, that no matter what
right triangle you form, the orthocenters will lie on a vertex and the centeroids
will lie on the midpoint of the side opposite of the right angle.
.
This investigation is a unique one.
Return to Kelly's Home Page.