A parametric curve is a pair of functions
where the two continuous functions define ordered pairs (x,y). The extent of the curve is dependent on the range one sets for t.
When looking at parametric equations, there are a couple of things one can get out of just the equations without even graphing them. In this discussion, the parametric equations that are explored are linear parametric equations or parametric equations of a line as they are more commonly called. If given two parametric equations
what can be understood from them before graphing them. The first thing
to notice is that the slope of the line that these two parametric curves
define is equal to
. This is illustrated in Figure 1
below.
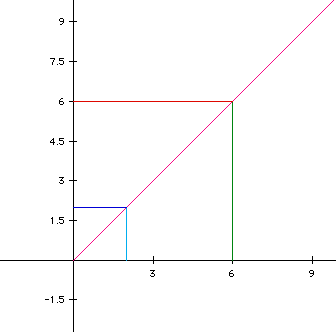
The pink line above is the graph of the parametric equations
The values of a and c are zero, b and d are 1, and t was in the range from 0 to 10. From this figure, notice that when x=2, y=2 and when x=6, y=6. This tells you that the slope of the line must be 1, which satisfies the statement above that the slope was the quotient of d and b. Another piece of information that one can obtain from two parametric equations that define a line, is the point at which the graph will start. In Figure 1, the values of a and c and the initial value of t was zero and thus the point at which the graph started was (0,0). So one would think that these points have something to do with were the graph starts and in fact they will define exactly where the graph will start. If the value of t is zero, then the point at which the graph starts will be (a,c). Figure 2 shows a graphical description of this.
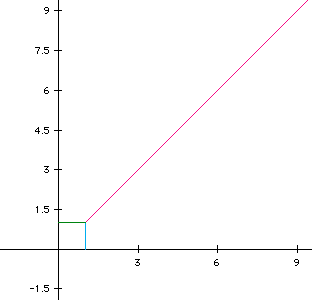
From looking at this graph, one will notice that the graph does not start at (0,0) therefore a and c must not equal zero. The parametric equations for Figure 2 are
for a range of t between 0 and 10. Since t=0 is the first time that becomes, this yields the start point for the graph to be at (1,1), which is consistent with the graph in Figure 2. Therefore, when the initial time for t is zero, the starting point of the the graph will be located at (a,c). Where would you expect the graph to start when the initial value of t is not zero? The answer to this comes right out the what was just discussed. To find the starting point of the graph of parametric equations of a line, one must only add the value of t to the value of a and the value of c, and these two new values will be the coordinates of the starting point. Or more simply, the starting point of the graph of parametric equations of a line will be located at (t+a,t+c).
Now that we know how to determine what the slope and starting point will be for parametric equations of a line, we will know try to solve the following problem: Write parametric equations of a line that pass through (5,7) with a slope of 3. You know that there can only be one line that is defined from positive infinity to negative infinity that passes through (5,7) with a slope of 3. However, parametric equations allows us to break this one line down into smaller segments but the segments that we define must still pass through (5,7) with a slope of 3. There are many different equations one could write to satisfy this problem. All of the solutions listed here take into account that t varied from 0 to 10.
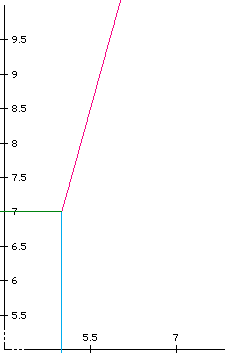
Figure 3 is the graph of the parametric equations
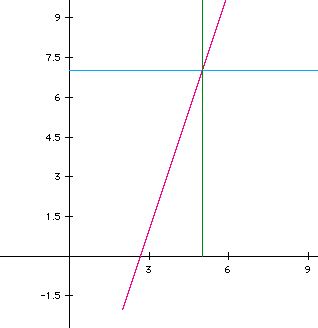
From this figure you can see that the graph (we are talking about the pink line in the graph) starts at point (a,c) and has a slope of 3 and passes through the point (5,7). The green line is the line x=5 and the aqua line is the line y=7. These lines were included to show that the point (5,7) does in fact lie on the parametric equations of a line defined for this graph. Figure's 4 and 5 show two more examples of paramtric equations of a line that have slope 3 and pass through the point (5,7). The equations represented in the two graphs are
respectively.
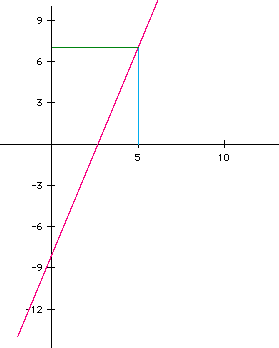
The examples of parametric equations of a line given here are just three
of the many possibilities one can form. An easy way to form pairs of parametric
equations that fit the requirements of passing through (5,7) and have a
slope of three is to determine one of the equations first. Then solve this
equation to find out at what value of t the parametric equations
of a line will be located at the point on the line that was given as a requirement.
Then take this time and the fact thatmust equal the required
slope to find the other equation. Once a pair of equations is formed, you
can get many different variations of those equations by simply changing
the value of t to start and stop the graph of different times. All
of the graphs will be using the same pair of equations, but the line segment
that they define will be different for each different value of t.
Parametric equations of a line are only one family of parametric equations. Some of the other families of parametric equations create some really odd shapes. It is left up to the reader to explore the many other possibilities of aprametric curves.