

The following explorations on based the standard form of the parabola
and what happens to the graphs as one changes the values of a, b and
c. The easiest way to see how a parabola's graph depends on a, b and c is
to keep two of them fixed and vary the third.
What would you expect to happen to the graph of a parabola as the value of c is varied while keeping both a and b fixed. Will the parabola become wider, thinner, shift up, down, left or right etc. Figure 1 below shows the graph of multiple parabola's with varying values for c while keeping both a and b fixed.
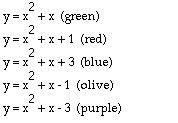
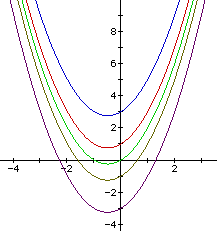
From Figure 1 one can see that varying values for c while
keeping both a and b fixed, shifts the parabola up or down.
This can be understood by letting x = 0. With x = 0, the value
of y becomes the value of c (in other words where the parabola
crosses the y-axis). From this you notice that when x = 0, the point
on the graph is (0,c). So when given a set of parabola's, if a
and b are the same for each parabola you can determine the order
in which the parabola's will be displayed when graphed without actually
graphing them.
Now that we know what happens when varying values for c while keeping both a and b fixed, what would you expect to happen to the graph of a parabola as the value of b is varied while keeping both a and c fixed? Once again, will the parabola become wider, thinner, shift up, down, left or right etc. One would assume that varying b would not shift the parabola's up or down since that is what c does. Figure 2 shows the graphs of multiple parabola's with varying values for b while keeping both a and c fixed.
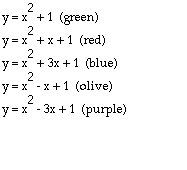
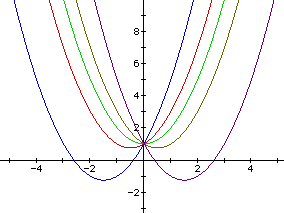
Is this what you had predicted would happen? From Figure 2, one can
see that varying b while keeping a and c fixed moves
the parabolas left or right on the x-axis. From the graphs you can get that
for b<0, the parabola's shift to the left and for b>0,
the graphs shift to the right. Also notice that all the parabolas have one
point in common. This is the point (0,c). Furthermore, as b
moves away from zero in both directions the parabolas move down as well
as left or right. This happens because the shape of the parabolas are not
changing and each parabola must still pass through the point (0,c),
and inorder to still pass through the point the parabolas must also shift
down otherwise they would not all have a point in common.
Finally let's explore the consequences of varying a while keeping
both b and c fixed for a set of parabolas. What do you think
will happen this time? Figure 3 shows the graphs of multiple parabola's
with varying values for a while keeping both b and c fixed.
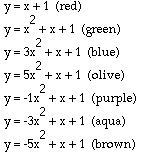
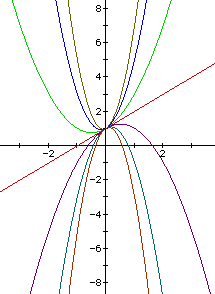
Compare these results to those that you predicted. How correct were your
hypothesis'? There are a number of interesting happenings to parabolas when
a is varied and both b and c remained fixed. One such
intersting happening is when a=0, this reduces the parbola to a stright
line as seen above. Also, while a is positive the parabolas are concave
up and when a is negative the parabolas are concave down. This comes
from the second derivative of the equation of the parabola. Continueing
on, as a moves away from zero in both directions the parabolas become
skinnier and skinnier(or as a moves closer to zero from the positive
or negative side the parabolas become wider and wider until at zero the
parabola becomes a straight line). This occurs because as a becomes
larger(or smaller if talking about negative values of a) the value
of x does not have to be as large to make y become large.
Thus having a smaller value of x and larger value of y and
when these points are plotted the parabolas become skinnier(or steeper)
faster.
These three explorations are just a few of the many explorations one can
do with parabolas. I will leave it up to the reader to explore other cases
that may be of interest to them.