

The following explorations will be of the centers of the orthic triangle. Given a triangle, the new triangle formed from connecting the feet of the altitudes of the given triangle is the orthic triangle. An altitude of a triangle is a perpendicular segment from a vertex to the line of the opposite side. There will be four centers of a triangle that will be referred to many times in these explorations. They are the
For a better understanding of the centroid, orthocenter, circumcenter and incenter, follow the links below.
 Click on the image to see a larger
version.
Click on the image to see a larger
version.
Click here to see how the centroid moves for different shapes and sizes of triangles.
 Click on the image to see a larger
version.
Click on the image to see a larger
version.
Click here to see how the orthocenter moves for different shapes and sizes of triangles.
 Click on the image to see a larger
version.
Click on the image to see a larger
version.
Click here to see how the circumcenter moves for different shapes and sizes of triangles.
 Click on the image to see a larger
version.
Click on the image to see a larger
version.
Click here to see how the incenter moves for different shapes and sizes of triangles.
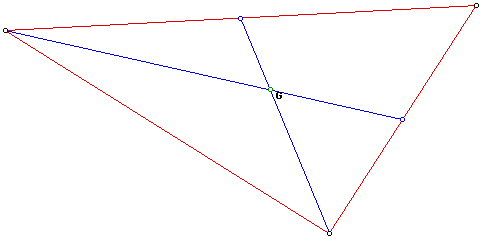
Now that the centroid, orthocenter, circumcenter and incenter have been defined we can move on to the theme of these explorations the orthic triangle. To start take a look at the orthic triangle below.
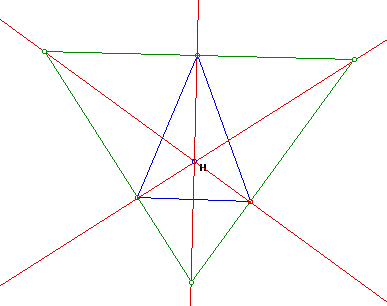 Click on the image to see a larger version.
Click on the image to see a larger version.
Click here to see how the incenter moves for different shapes and sizes of triangles.
Now we can explore the centers and Euler lines of both the orthic triangle and triangle RST(the triangle that defined the orthic triangle).
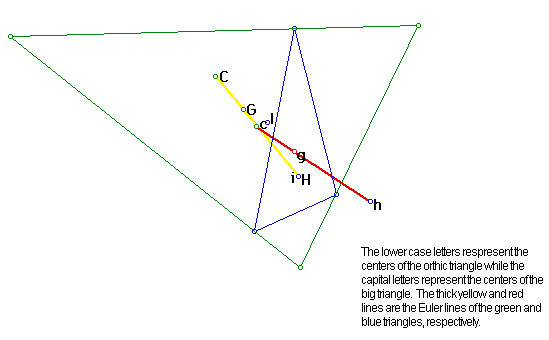 Click on the image to see a larger
version.
Click on the image to see a larger
version.
Click here to see how the orthic triangle changes shape for different shapes and sizes of triangles.
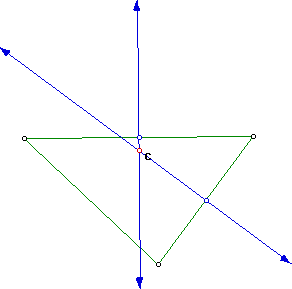
The first thing to notice is that the c(the circumcenter of the orthic triangle) is the midpoint of the Euler line of triangle RST. This is illustrated in the image below.
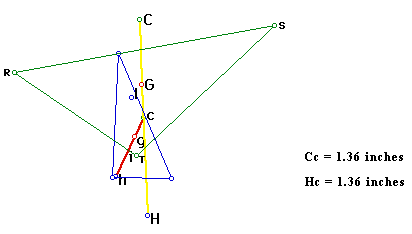
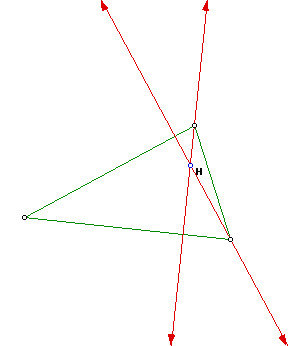
Furthermore, notice that for an acute triangle RST, the orthocenter(H) of triangle RST is the same point as the incenter(i) of the orthic triangle. This can be seen in the picture below. The dotted lines are the altitudes of triangle RST and thus intersect one another at H(the orthocenter of triangle RST). The incenter is defined as the common intersection of the angle bisector of each angle. Looking at the angle measurement given in the picture below, you can see that angle UWV is twice as large as angle UWR. This tells you that the dotted line that passes through points R and W is an angle bisector of the orthic triangle. The angle VUW is also twice as large as angle VUS, therefore the dotted line that passes through points S and U is also an angle bisector of the orthic triangle. Since the altitudes of triangle RST are on the same lines as the angle bisectors of the orthic triangle, the orthocenter(H) of triangle RST is the same point as the incenter(i) of the orthic triangle. This is only true; however, when triangle RST is an acute triangle.
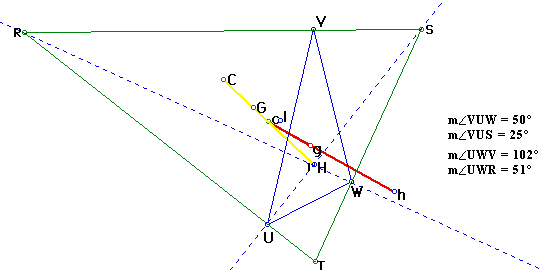
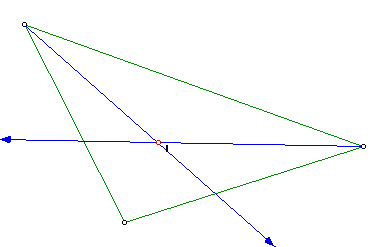
Another similarity between triangle RST and the orthic triangle occurs when triangle RST is an obtuse triangle. As can be seen below, point T, which is a vertex of triangle RST, is the incenter of the orthic triangle. As in the proof used above, from the angle given in the picture below one can see that angle VUW is twice as large as angle RUW. This tells you that the dotted line that passes through points R and U is an angle bisector of the orthic triangle. The angle WVU is also twice as large as angle VST, therefore the dotted line that passes through points V and T is also an angle bisector of the orthic triangle. Since the angle bisectors of the orthic triangle intersect one another at point T on triangle RST, the incenter(i) of the orthic triangle and point T(one of the vertices of triangle RST are concurrent. Thus T is the incenter of the orthic triangle when triangle RST is an obtuse triangle.
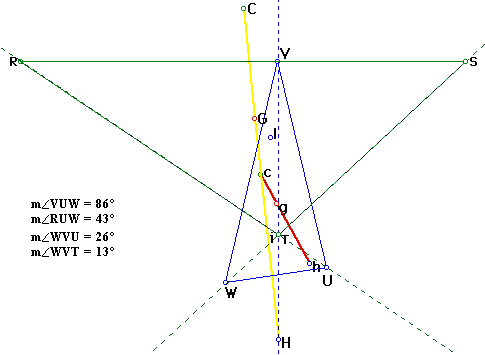
What do you think the consequence will be when triangle RST is a right triangle? What will the centers of triangle RST and the its orthic triangle have in common? Determine your outcome and then see what the right triangle RST creates.
There are many other similarities between the centers of both triangle RST and its orthic triangle. What happens when triangle RST is isoceles? Equilateral? Using GSP allows one to investigate these and many more.