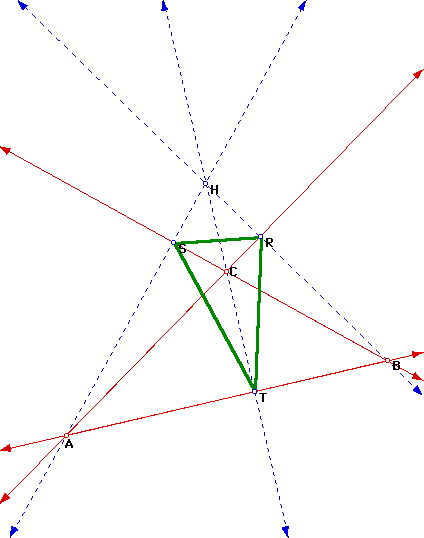
When the pedal point is located at the orthocenter of triangle ABC, the pedal triangle becomes the orthic triangle. This is illustrated in the picture below by the altitudes(in blue) of triangle of ABC. Since the orthic triangle is the triangle connecting the feet of the altitudes, one will notice that the feet of the altitudes are the vertices of the pedal triangle thus the orthic triangle and the pedal triangle are the same triangle when the pedal point is located at the orthocenter.

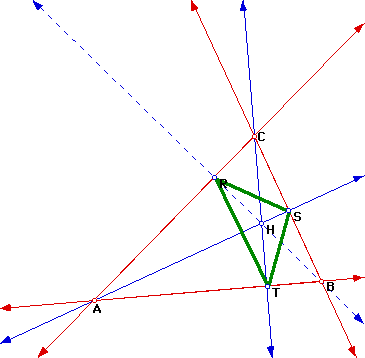
If the orthocenter is located outside of triangle ABC, the pedal triangle is still the same as the orthic triangle as is evident from the image below. Another point worth mentioning about the pedal triangle(or orthic triangle since they are the same triangle) is that when the orthocenter is outside triangle ABC, the vertice of triangle ABC that is the vertex of the obtuse angle of ABC becomes the incenter of the pedla triangle(or orthic triangle). The proof of this can be found in a discussion on Centers of an Orthic Triangle.