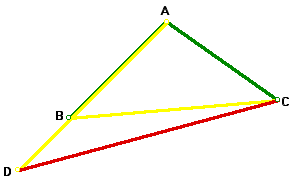
Problem: 100 degree Isosceles Triangle |
Given an isoscles triangle ABC with AB = AC and the measure of angle BAC = 100 degrees. Extend AB to point D such that AD = BC. Now draw segment CD. What is the measure of angle BCD?
Note: The segments in this figure are color coded according to which segments are congruent to which other segments.

Since triangle ABC is isosceles with AB=AC and angle BAC=100 degrees, each of the base angles (angle ABC and angle ACB) must each be 40 degrees because base angles of an isosceles triangle are congruent. Now, I will construct an equilateral triangle ADE as in the figure below. Once again, the segments are colored coded according to which segments are congruent to one another.
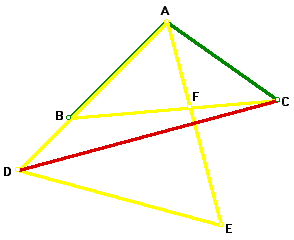
From this figure, we can see that angle CAF plus angle BAF equals 100 degrees. Since angle BAF=60 degrees, angle CAF must be 40 degrees. This tells us that angle CAF and angle ACF are congruent, thus triangle AFC is isosceles also. With triangle AFC being isosceles, AF=CF.
Now, EF + FA = CF + FB because AE = BC. Since CF = FA, we are left with EF = BF by the properties of segment addition. We also know that angle AFB = angle CFE because they are vertical angles. Therefore, triangle CFE is congruent to triangle AFB. From this, one gets that CA = CE, by corresponding parts of congruent triangles are congruent. Our figure now looks like this:
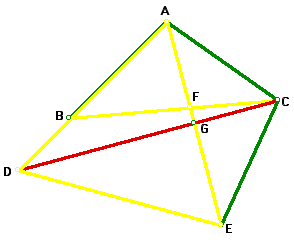
Now we have triangle ADC congruent to triangle EDC. These two triangles form a kite and by the property of a kite, the red segment CD is a perpendicular bisector of segement AE. This tells us that all four angle around point G are right angles. We know that angle EFC measures 80 degrees because angle AFC measures 100 degrees and they are supplementary. Now in triangle FGC, we have angles of 80 and 90 degrees so the third angle must be 10 degrees.
Therefore, angle BCD = 10 degrees.
Questions, Comments or
Suggestions
©1998 by Luke Rapley