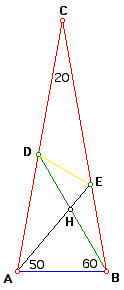
Problem: 20 Degree Isosceles Triangle |
Given the isosceles triangle below with AC = BC, angle C = 20 degrees, angle ABD = 60 degrees and angle BAE = 50 degrees, determine the measure of angle EDB.

The first thing I will do is draw segment DG parallel to AB. Then construct segment AG. This along with the construction of segment FE is illustrated in the figure below.
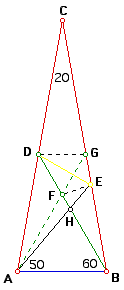
From this drawing, I will determine the measure of angle EDB.
In triangle ABE, angle EAB = 50 degrees and angle EBA = 80 degrees; therefore, angle BEA = 50 degrees. This tells us that triangle ABE is an isosceles triangle with AB = EB.
Triangles AGB and BDA are congruent by SAS (Side-Angle-Side). Therefore, angle DBA = angle GAB. Also, angle BAG = angle AGD because they are alternate interior angles of transversal that cuts 2 parallel lines.
Now, we have angle AGD = angle BDG = angle DFG.
So triangle FDG is equilateral with FG = DG = DF.
Angle AFB = 60 degrees because it is a vertical angle to angle DFG. Therefore, triangle AFG is equilateral with AB = FB = FA.
Earlier, I stated AB = EB. From this we see FB = EB and triangle EFB is isosceles with base angles FEB and EFB having measures of 80 degrees.
Since angle DFG = 60 degrees and angle BFE = 80 degrees, angle GFE = 40 degrees. Thus, FE = GE because they are both siddes of an isosceles triangle.
Now, DGEF is a kite and DE bisects angle GDF by the property of a kite.
Therefore, angle EDB = 30 degrees because angle GDF = 60 degrees (the measure of an angle in an equilateral triangle).
In this solution, the first thing I will do is construct part of circle with point B as its center and BD as its radius such that the circle meets line BA at point F and meets segment BC at point G. This construction is illustrated in the figure below.
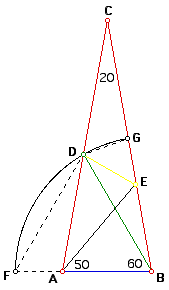
From this figure, one can see that FB = DB because they are both radii of the circle. Therefore, we have an isosceles triangle FBD with a 60 degree angle which implies that triangle FBD is equilateral. Thus, angle F = 60 degrees and angle FDA = 20 degrees.
Angle DBC = 20 degrees and thus triangle BDC is isosceles with BD = CD. BD = FD because triangle FBD is equilateral and therefore FD = CD by transitivity.
Since angle AEB = 50 degrees, triangle ABE is isosceles and AB = EB. Furthermore, FA = GE by segment addition.
Also, BD and BG are both radii of the circle, thus they are congruent and triangle DBG is isosceles with BG = BD. This implies that angle BDG = 80 degrees, angle BGD = 80 degrees and angle DBC = 100 degrees.
Now, triangle FDA is congruent to triangle DCG by A.A.S. From this, we determine that FA = DG because corresponding parts of congruent triangles are congruent. This then gives us DG = EG, which implies that triangle DGE is isosceles.
Knowing this, angle EDG = 50 degrees.
Since, angle BDG = 80 degrees and angle EDG = 50 degrees, angle EDB = 30 degrees.
Questions, Comments or
Suggestions
©1998 by Luke Rapley