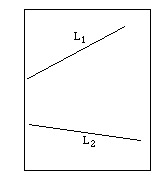
Imagine a sheet of paper with two line segments drawn on it, as shown. Without extending the paper or the line segments, construct the bisector of the angle determined by the two line segments.

How many different solutions can you find?
The first thing is to draw any segment between L1 and L2 such that the endpoints of this segement line-on L1 and L2. This is illustrated in the diagram below.
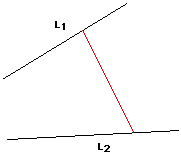
We now have two vertices of a triangle and if we knew where the third vertice was we could construct the angle bisector. The reason for drawing the red segment is because we want to create an isosceles triangle and we need to know what the measure of the base angles needs to be.
Next, copy the angle formed by the red segment and L2 and add it to the angle formed by the red segment and L1. Now, we can draw a new segment that represents the total angle. This step is shown in the figure below. The blue segment represents this new segment.
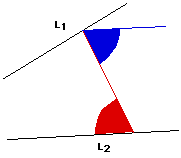
The angle marked in red is the angle that was copied to the position of the angle marked in blue. The obtuse angle formed by L1 and the blue segment has the measure of the sum of the two base angles of a triangle. If this triangle is isosceles, then each of the base angles has the same measure. So, the next step will be to bisect this angle and construct the two base angles of an isosceles triangle. The reason we want to construct an isosceles triangle is because we know that the angle bisector of the one angle that is not a base angle of an isosceles triangle is a perpendicular bisector of the side included by the base angles. Therefore, once we have the base angles for an isosceles triangle, we can construct the side included by them and then construct the perpendicular bisector of this side and we will have the angle bisector.
The figures below illustrate bisecting the obtuse angle formed by L1 and the blue segment, copying this angle to both L1 and L2 and constucting the segment included by these two new angles.
Figure 1`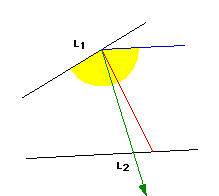 |
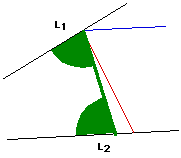 | |
The green ray in Figure 1 above resembles the angle bisector of the angle marked in yellow. Figure 2 illustrates copying the bisected angle to both L1 and L2 and then constructing the segment from the point of intersection of the L1 and the green ray and the point of intersection of L2 and the green ray. Now, we have the side included by the base angles of an isosceles triangle (the solid green segment in Figure 2). All that we need to do now is find the perpendicular bisector of this green segment and we will have the angle bisector of the original two segments that we were given. This perpendicular bisector is shown in the figure below.
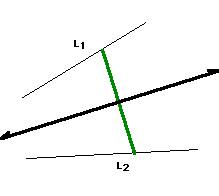
Questions, Comments or
Suggestions
©1998 by Luke Rapley