Brahmagupta's formula is provides the area A of a cyclic quadrilateral (i.e., a simple quadrilateral that is inscribed in a circle) with sides of length a, b, c, and d as

where s is the semiperimeter

---

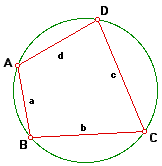
Before getting started, I will make a couple constructions on the figure above. I will extend segment DA and segment CB such that they intersect at a point P. This is illustrated in the figure below.

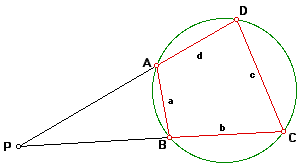
If we let segment PC = x and segment PD = y, the area of triangle PDC can be given by Heron's formula as,

,

	'
	. ( I )

Now, from this figure angle ADC is supplementary to angle ABC because they are opposite angles of a cyclic quadrilateral. Angle ABP is also supplementary to angle ABC, thus angle ABP = angle ADC. This implies that triangle PBA and triangle PDC are similar because their angles are congruent.

Since we have two triangles that are similar, we can set up some ratios.

,
,
. ( II )

Similarly,

and . ( III )

Thus,

, ( IV )
a(x+y) = c(x+y) - c(b+d),

(c-a)(x+y) = c(b+d),
,
,
. ( V )

This is a solution for one of the terms in the area function ( I ) of triangle PDC from above. If we find the solution for the other terms in equation ( I ), we can then solve for the area of ABCD.

Using similar methods to III and the steps that follow IV above, one would arrive at equations for (y+c-x), (x+c-y) and (x+y-c).

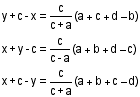	( VI )
	( VII )
	( VIII )

Now, by substituting (V), (VI), (VII) and (VIII) into (I) we arrive at

area of triangle PDC =. ( IX )

By rewriting (II), one can see that area of triangle PDC =*(area ABCD). ( X )

Now, if we equate (IX) and (X), we get

.

This is can be simplified to . This is Brahmagupta's formula for the area of a cyclic quadrilateral with s equal to the semi-perimeter as stated above.

Questions, Comments or Suggestions
©1998 by Luke Rapley