

Given a rectangular sheet of cardboard 15 in. by 25 in. If a small square of the same size is cut from each corner and each side folded up along the cuts to from a lidless box:
What is the maximum volume of the box?
What size(s) of the square would produce a box of volume equal to 400 cubic inches?
Figure 1 shows an illustration of the box that we need to form.
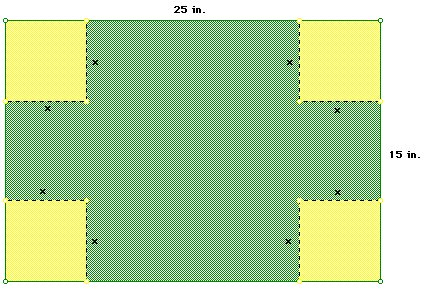
The first thing to realize from this figure is that the size of the square that is to be cut from each corner must be less than 7.5 in by 7.5 in. This is true because if the size of the square was 7.5 in by 7.5 in. no box could be formed because the width would be zero and the size of the square cannot be greater than 7.5 in by 7.5 in. because one would not be able to cut an equal size square out of each corner because the width of the cardboard that we are given is only 15 in.
There are a couple of different ways one can go about solving the two problems asked above. One could answer them graphically, with the help of a spreadsheet, using hand written mathematics and solving equations, etc. The graphical and spreadsheet methods will be used here. In order to get a graphical representation of this problem we need an equation for the volume of the box. Looking back to Figure 1 to determine the length, width, and height, the equation for the volume of the box that needs to be solved is V=(25-2x)(15-2x)x. Simplified this is V = 4x^3 - 80x^2 + 375x. Now graphing this equation (remembering that x must be less than 7.5 in.) we get a nice curve that shows that there is a maximum. Figure 2 shows this graph.
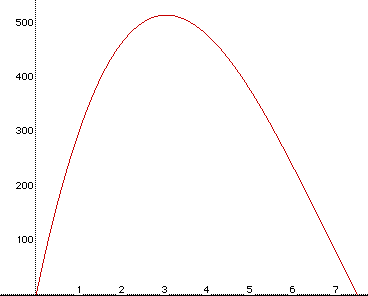
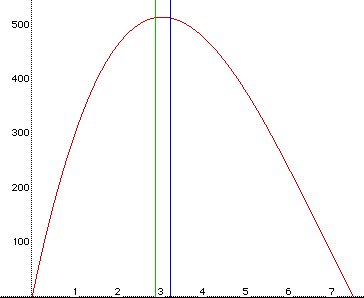
From this figure, notice that the maximum volume is a little over 500 cubic inches and this occurs when the size of the square cut out of each corner is about 3 in. by 3 in. Now we have narrowed down the range for which the size of the square cut from each corner can be. It is in the range between 2.9 in. and 3.25 in. square. This is seen in Figure 3. The lines for x=2.9 in. and x=3.25 in. are shown and the maximum volume is between these two x-values.
Now with the range narrowed down, we can go to a spreadsheet program and let the spreadsheet do the calculations for many different possible values of the size of the square to be cut out and determine the size of the square that when cut out creates a box a greatest volume. One way to do this is to put in one column values of the width of the square to be cut out, starting with 2.9 in. and increasing this by some increment up to the 3.25 in. Then in another column determine the volume for each of these values. Then look at the different volumes that were just calculated and find the values of the width of the square where the volume is going up, then levels off and then starts going back down. Now use the smallest of these three widths and create another column similar to the first column you created but you only need to let the widths of the square range between the the smallest and largest of the three widths you just determine to be the ones that zeroed in on the maximum volume. With multiple repetitions of this one can find a value for the width of the square that will give the greatest volume. With each repetition, you gain one more decimal place of accuracy. Table 1 below illustrates the initial calculation of the volume of the box for values of the width of the square between 2.9 in. and 3.25 in.
| Side of Square(in.) | Volume in Cubic Inches | Side of Square(in.) | Volume in Cubic Inches |
| 2.900 | 512.256 | 3.080 | 512.960 |
| 2.910 | 512.370 | 3.090 | 512.917 |
| 2.920 | 512.476 | 3.100 | 512.864 |
| 2.930 | 512.573 | 3.110 | 512.803 |
| 2.940 | 512.661 | 3.120 | 512.733 |
| 2.950 | 512.740 | 3.130 | 512.655 |
| 2.960 | 512.809 | 3.140 | 512.569 |
| 2.970 | 512.870 | 3.150 | 512.474 |
| 2.980 | 512.922 | 3.160 | 512.370 |
| 2.990 | 512.966 | 3.170 | 512.258 |
| 3.000 | 513.000 | 3.180 | 512.138 |
| 3.010 | 513.026 | 3.190 | 512.009 |
| 3.020 | 513.042 | 3.200 | 511.872 |
| 3.030 | 513.051 | 3.210 | 511.727 |
| 3.040 | 513.050 | 3.220 | 511.573 |
| 3.050 | 513.041 | 3.230 | 511.411 |
| 3.060 | 513.022 | 3.240 | 511.241 |
| 3.070 | 512.996 | 3.250 | 511.063 |
The three rows highlighted in green in Table 1 correspond to the three values of the width of the square where the volume is increasing, levels off and starts to decrease. These values were then broken up again like the ones in Table 1 but with one more decimal place of accuracy. After repeating Table 1 a couple more times, a value of x(the width of the square to be cut from each corner) equal to 3.03425 was determined to give the greatest volume of the box. With more iterations of Table 1, one could get a value for x that has more decimal places. This value of x=3.03425 in. makes the volume of the box become V=513.0512959596 cubic inches.
Now to answer the other question about, what size(s) of the square would produce a box of volume equal to 400 cubic inches, we can turn again to the graph in Figure 2. Since we want a volume of 400 cubic inches, if we draw the line corresponding with V=400 on the graph in Figure 2 we will end up with a graph that looks like the one in Figure 4.
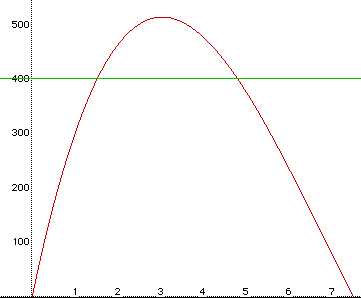
The intersection points of the curve and line in Figure 4 represent the two values of the width of the square when cut from the corners of the piece of cardboard will generate a volume equal to 400 cubic inches. These intersections look as though they occur at about x=1.5 and x=4.75. Now we will need to go through the steps done above to find the value of x that gave the largest volume to find the values of x that give a volume of 400 cubic inches. These steps will need to be performed on x=1.5 and then on x=4.75.
After going through the same process as above to find the value of x, the two values of x that make the volume of the box equal 400 cubic inches are x=1.5249288 in. which gives a volume of V=399.999998 cubic inches and x=4.7928497 in. which gives a volume of V=400.0000063 cubic inches. These values for the volumes are not exactly equal to 400 cubic inches but are very close. One could get the volumes even closer to 400 cubic inches simply by repeating the steps used in Table 1 more times on this data.
The methods used here to determine the values of x that were required to satisfy the two questions asked were just two of the many different ways of determining them. Explore other methods as your mind contemplates the ones shown here.