Assignment 5
Geometer Sketchpad
Scripts
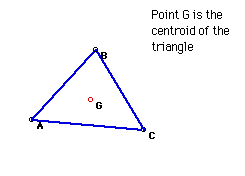
1. Centroid
The centroid (G) of a triangle the common intersection of the three
medians. A median of a triangle is the segment from a vertex to the midpoint
of the opposite side.
Click on the picture to explore the location of the centroid for various
triangles.
Click Here to see the script for the construction of the centroid of
a triangle.
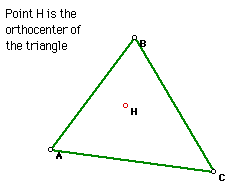
2. Orthocenter
The orthocenter (H) of a triangle is the common intersection of the
three lines containing the altitudes. The altitude is a perpendicular segment
from a vertex to the line of the opposite side.
Click on the picture to explore the location of the orthocenter for various
triangles.
Click Here to see the script of the construction
of the orthocenter of a triangle.
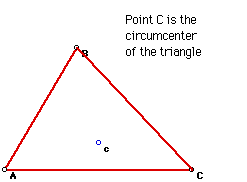
3. Circumcenter
The circumcenter (C) of a triangle is the point in the plane equidistant
from the three vertices of a triangle. Since a point equidistant from two
points lies on the perpendicular bisector of the segment determined by two
points, C is on the perpendicular bisector of each side of the triangle.
Click on the picture to explore various locations of the circumcenter
for various triangles.
Click Here to see a script for the construction
of the circumcenter of a triangle.
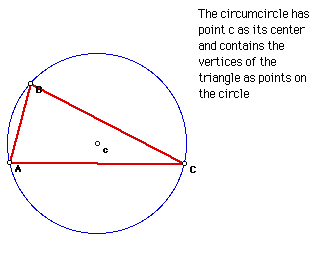
4. Circumcircle
The circumcircle is created with the circumcenter (C) as its center.
The vertices of the triangle are located on the circumcenter.
Click the picture to explore the circumcircle for various triangles.
Click Here to see a script of the construction
of the circumcenter of a triangle.
5. Incenter
The incenter (I) of a triangle is the point on the interior of a triangle
that is equidistant from the three sides. Since a point interior to an angle
that is equidistant from the two sides of the angle lies on the angle bisector,
then I must be on the angle bisector of each angle of the triangle.
Click the picture to explore the location of the incenter for various
triangles.
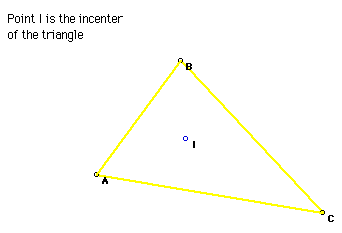
Click Here to see a script for the construction
of the incircle of a triangle.
6. Incircle
The incircle of a triangle is constructed with the incenter (I) as the
center. The radius of the incircle is a perpendicular segment from the incenter
to a side. The incircle is tangent to the sides of the triangle.
Click the picture to explore the incircle of various triangles.
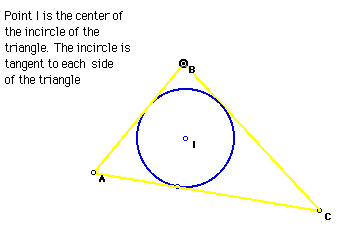
Click Here to see a script for the construction
of the incircle of a triangle.
7. Medial triangle
The medial triangle is created by connecting the midpoints of a triangle.
Click the picture to explore the properties of the medial triangle for various
[original] triangles.
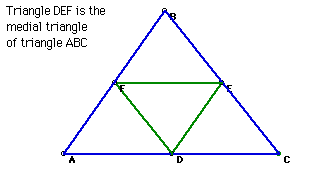
Click Here to see a script for the
construction of a medial triangle.
7a. Orthocenter, Mid-segment triangle.
The orthocenter, mid-segment triangle is created by connecting the midpoints
of the segments HA, HB, and HC.
Click the picture to explore the properties of this triangle.
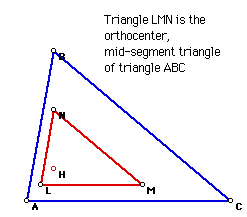
Click Here to see a script
for the construction of a triangle created by the midsegments of the orthocenter
and the original triangle.
8. Orthic triangle
The orthic triangle is constructed by connecting the feet of the altitudes
of a triangle.
Click the picture to explore the properties of the orthic triangle.
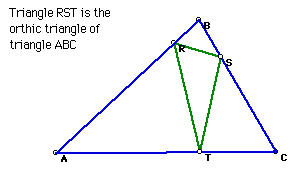
Click Here to see a script of the construction
of the orthic triangle.
9. Pedal triangle
The pedal triangle is created by selecting an arbitrary point (p) that
can be either inside or outside the triangle. The triangle is created by
creating a perpendicular line from the lines that create the original triangle
to the pedal point. The intersection of these lines is then used to form
the pedal triangle.
Click the picture to explore the pedal triangle for various [original] triangles.
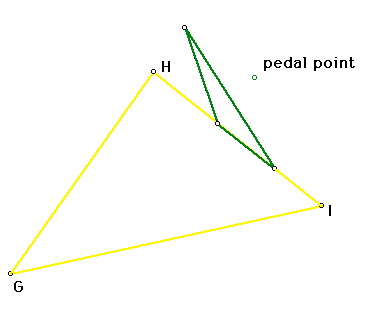
Click Here to see the script for the
construction of the pedal triangle for any triangle.
10. Center of Nine point circle
The nine point circle is created by the midpoints of AB, BC, and AC;
the points at the feet of the altitudes; and the midpoints of the segments
connecting the vertices of triangle ABC to the orthocenter.
Click the picture to explore the points on the nine point circle for
various triangles.
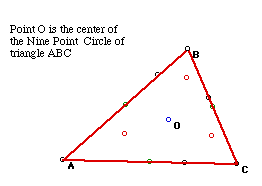
Click here to see a script for the construction
of a nine-point circle.
11. Nine Point Circle
The nine point circle is created by the midpoints of AB, BC, and AC;
the points at the feet of the altitudes; and the midpoints of the segments
connecting the vertices of triangle ABC to the orthocenter.
Click the picture to explore the points on the nine point circle for
various triangles.
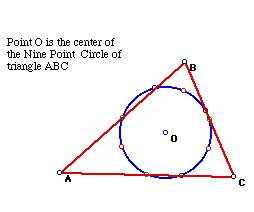
Click here to see a script for the
construction of a nine-point circle.
12. Trisecting a line segment
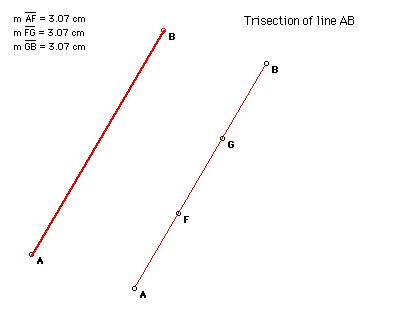
Click Here to see a script for
the trisection of a line segment.
13. Equilateral triangle, given a side
An equilateral triangle is a triangle whose sides are equal. The triangle
ABC was constructed using the given side AB.
Click the picture to manipulate the equilateral triangle for any length
AB.
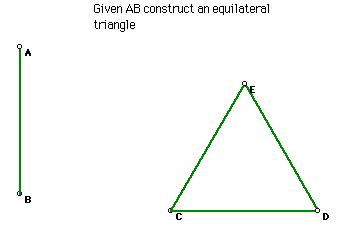
Click Here to see the script for
the construction of an equilateral triangle given the side AB.
14. Square, given a side
Click the picture to manipulate the square for any length of segment
AB.
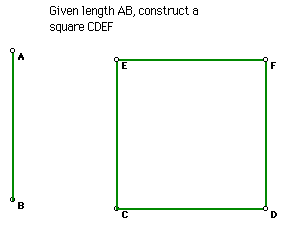
Click Here to see a script for the
construction of a square given a side.
15. Isosceles triangle, given base and altitude
An isosceles triangle is defined as a triangle that has two equal sides
and two equal bases.
Click the picture to manipulate the length of the base (MN) and the
altitude (QP) and the shape of the isoceles triangle.
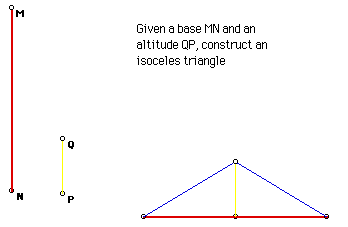
Click Here to see a script
for the construction of an isosceles triangle given a base and an altitude.
16. Triangle Centers (H, G, C, and I)
Click the picture to explore the locations of the centers of ABC for
various triangles.
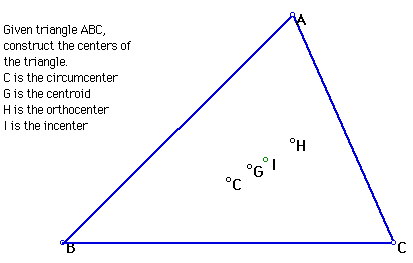
Click Here to see a script for the
construction of the centers of a triangle.
17. Triangle Centers (H, G, C, and I) with the Euler Line
Click the picture to explore the location of the centers of ABC and
the Euler Line for various triangles.
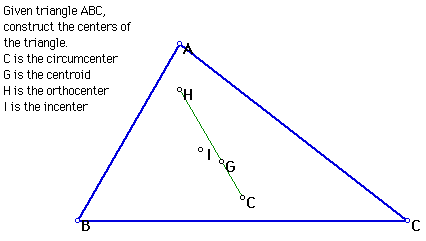
Click Here to see a script for the construction
of centers of the triangle ABC.
18. Locus of vertex of a fixed angle that subtends a fixed segment.
Click the picture to find the locus of the vertex of a fixed angle that
subtends a fixed segment (or look below to find out what the locus looks
like).
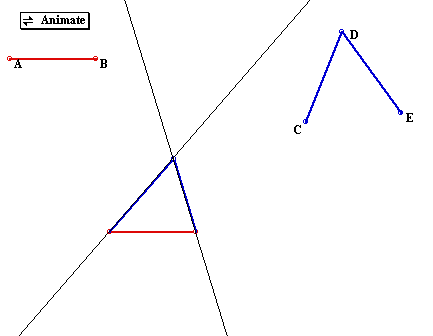
Click Here to see a script for the
construction of a fixed angle that subtends a fixed segment.
Below is a picture of the locus.

19. Divide a segment AB into two parts that form a golden ratio.
Click the picture to investigate line AB that has been divided into
the golden ratio.
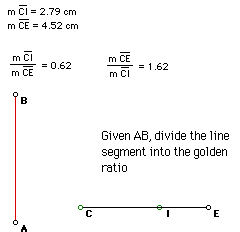
Click Here to see a script that allows
you to divide any segment into the golden ratio.
20. Pentagon, given a diagonal.
Click the picture to manipulate the length of AB and the size of the
pentagon.
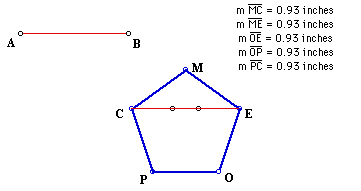
Click Here to see a script for
the construction of a pentagon given a diagonal.
21. Pentagon, given a radius.
Click the picture to manipulate the radius and the pentagon.
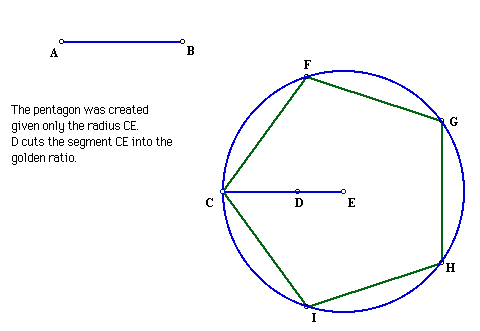
Click here to see a script for
the construction of a pentagon given a radius.
22. Pentagon, given a side.
Click the picture to manipulate line segment Q'R' and the size of the
pentagon.
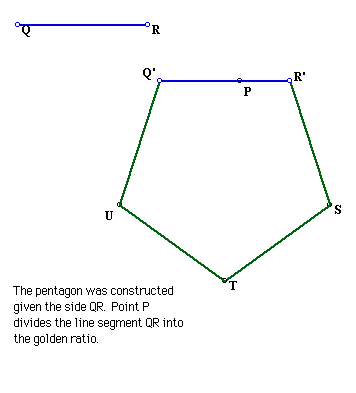
Click here to see a script for the
construction of a pentagon given a side.
23. Hexagon, given a side.
Click the picture to manipulate the length of AB and the size of the
hexagon.
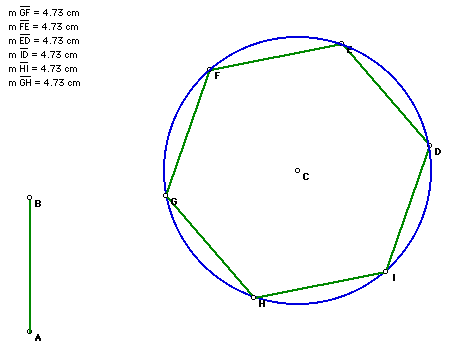
Click Here to see a script for the
construction a hexagon with a given side AB.
24. Octagon, given a side.
Click the picture to investigate the octagon given different lengths
of AB.
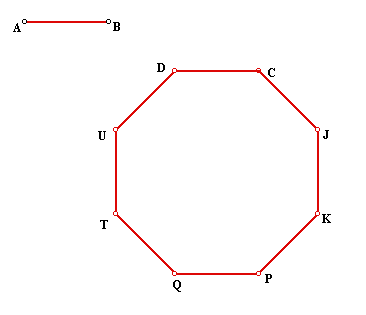
Click Here to see a script for the
construction of an octagon given a side.
25. Octagon, given a radius
Click the picture to investigate the octagon given different lengths
of CD.
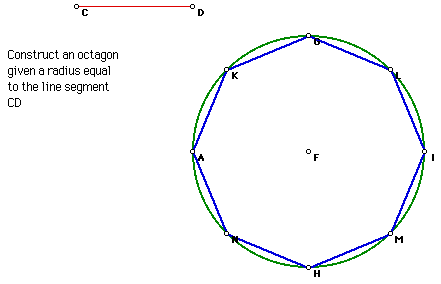
Click Here to see a script for
the construction of an octagon given a radius.
Return to my home page



























