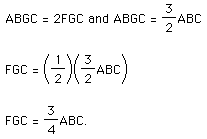
You may click on the picture to explore the locations and properties of the medians for various triangles.
Before we begin let's construct triangle ABC and its medians.
Medians are created by connecting each vertex with the midpoint of the opposite
side. Therefore, line segments AE, BD, and CF are the medians of the triangle
ABC.

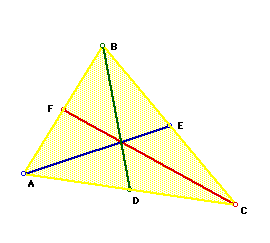
Our task is to explore the properties of each of the triangles and determine
if any relationships exist between the two triangles, and more importantly
if those relationships will hold for any triangle. We can use GSP to begin
our measurement of the two triangles. I am going to use the line segment
FC to use as the foundation for the construction of the new triangle. This
will, hopefully, bypass any inconsistencies in length due to cutting and
pasting of the segment.
Because we are using line segment FC as the static line from which we will
construct our new triangle, I will begin by creating a line that passes
through point F and is parallel to line segment AE. In turn, I will construct
a line that passes through point C and is parallel to line segment BD.
We can see that a triangle is created by the intersection of the parallel
lines. A construction of the line segments will create our new triangle.
You may click on the GSP image below to measure the lengths of the sides
of the new triangle to see in fact the lengths are indeed equal.
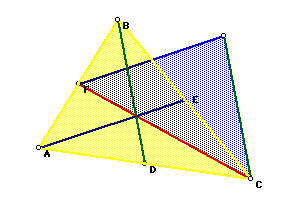
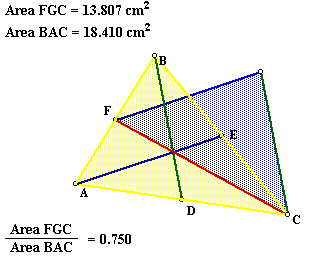
Now that our triangle is created we need to explore the relationships
that may or may not hold between the two triangles. An exploration using
GSP can help to find the data to investigate any relationships that may
exist.
Click Here to explore the triangles
using GSP.
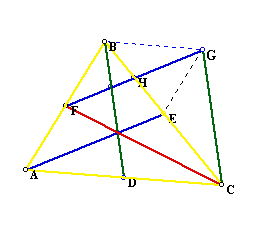
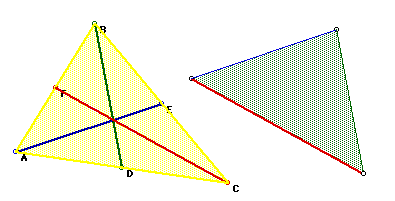
Constructing line segment BG and line segment GE has created the parallelograms BGCD and AFGE, respectively. The following images show the parallelograms shaded for clarity.
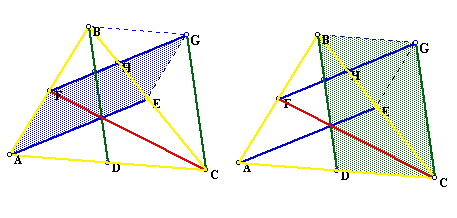
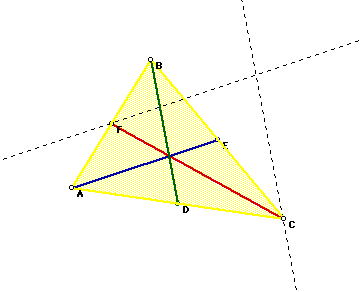
At this point, we would like to determine any relationships that may exist between the triangles ABC, FGC, and the new parallelograms. Because the area formula for any parallelogram is Area = (height)(base) we need to construct the height. The height (or altitude) is constructed by creating a line that is perpendicular to the base from a vertex of the parallelogram.
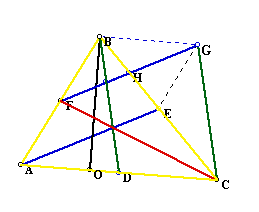
Therefore, BO is the altitude of the parallelogram BGCD. It is also the altitude of ABC.
Using this fact, we can determine:
Because BO is the altitude of the paralleloggram BGCD, we can also determine its area to be:
This leads to an interesting observation. The area for ABC and BGCD are very similar. If we look at our original picture, the similarity appears to be more than just an interesting fact. The line segment DC is half of the line segment AC, because of the fact that DC is created by the midpoint of AC. Therefore (1/2)AC = DC. Therefore the area of ABC equals the area of BGCD.
This fact can help us in our furthur investigations, since the triangle FGC seems to lie more in the area of the BGCD than in ABC.
The real "breakthrough" in solving the question at hand (how to prove that area of FGC is (3/4) the area of BAC, came when I looked at the "big picture". I decided to look at the formula for the area of the trapezoid BGCA. The following is the proof that "fell" out of the exploration of the trapezoid's area formula.

In the next image, I have created the midsegment of the trapezoid BGCA. The midsegment is constructed by connecting the midpoints of line segments BA and GC.
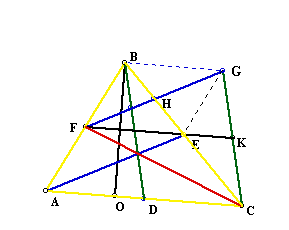
The midsegment FK, creates two distinct trapezoids FBGK and FKCA. The altitude (height) of each trapezoid is 1/2 of BO. We can mark that segment as BP, where the altitude intersects FK.
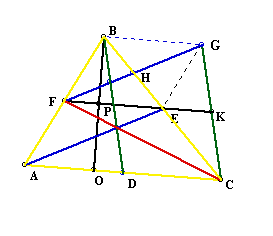
At this point, we want to prove that triangle FGC is 1/2 of ABGC. Triangle FGK and triangle FKC equal triangle FGC. This fact will help us in our final destination.
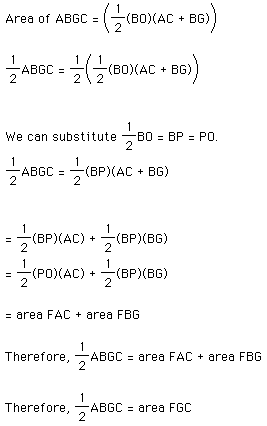
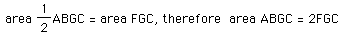
Our last part of the proof, brings together the relationships that we have proven above. The following can bring them together:
therefore: