
Over this image we construct triangle ABC's circumcircle. The circumcircle can be defined as a circle whose center is the circumcenter and contains the vertices of triangle ABC.
The last step in our construction is to create the new triangle LMN at the points of intersection of the angle bisectors and the circumcircle.
Our construction is complete. Now our investigation into the relationships of the angles begin. My first attempt at this exploration began with looking at a special triangle, namely the equilateral triangle. The observation that I made with this triangle is that the angles all had the same measure of 60 degrees. This could be considered fairly obvious since the angles in ANY equilateral triangle measure 60 degrees. What is important to note is that the angle degrees do not change even if the lengths of the sides of the triangle do. So, while the angle measurements will not show us any important information we can observe any relationships between their lengths which may help us in becoming closer to our goal.
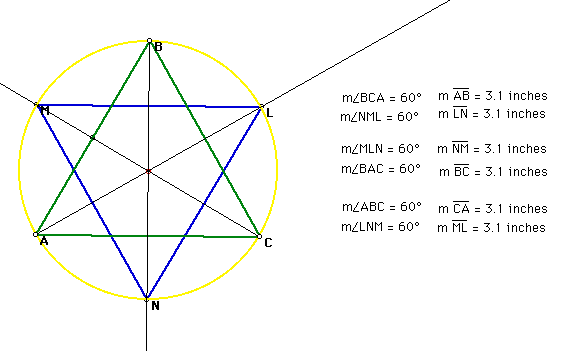
This image and its measurements show us that the lengths of the sides of triangle ABC are equal to the lengths of the sides of triangle LMN. This leads us to believe that there are some relationships worth investigating.
Furthur explorations prove that it is not the line segment that is important. If we changed the circle the angles would remain the same and the length of the sides would still be equal. The lengths however would change.
Let's take a look at the right triangle, another special triangle.
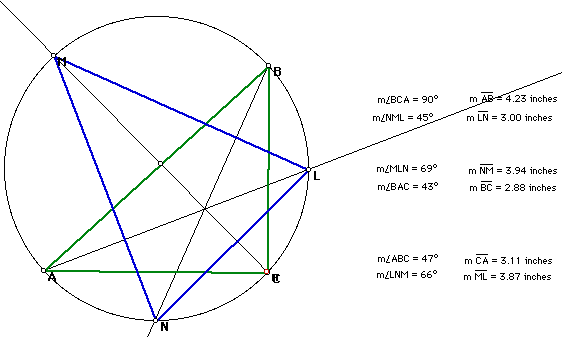
Looking at the measurements, there does not seem to be any relationship between the line segments and the angles opposite from them.
Let's turn our attention to the angles themselves. We created the angles through the construction of the circumcircle. If we look at the angle with more scrutiny we can see that the angles' vertex is a point on the circle and its rays intersect the circle in two distinct points other than the vertex. The aforementioned is the definition of an inscribed angle. All of the angles we created are inscribed.
An inscribed angle's measurement can be determined by looking at its intercepted arc (the arc created by its rays and the intersection of the circumcircle). An inscribed angle is 1/2 the measurement of its intercepted arc.
For instance, in our equilateral triangle the angles were all equal as were the lengths. The inscribed angles create three intercepted arcs. We can determine the measurement of the arcs by dividing 360 (the measure of the circle) by 3 (the number of arcs). Each arc measures 120 degrees. Therefore, the inscribed angle associated with it is 1/2 of 120 degrees or 60 degrees. These calculations (and the number of arcs) seem to suggest that there are only 3 inscribed angles that are being measured. The image shows us (and our construction proves to us) that there are, in reality, 6 inscribed angles.
If two or more inscribed angles intercept the same arc, they are considered congruent. We can look at the image of the equilateral triangle to see if this is the case. A closer inspection shows that each of the inscribed angles intercept a different arc whose measure is 120 degrees.
Our investigation continues trying to determine the relationship between the angles of our triangles. The image below will be explored because it is not a special triangle. Using the knowledge of the inscribed angles and their intercepted arcs may prove to be helpful in our next steps.
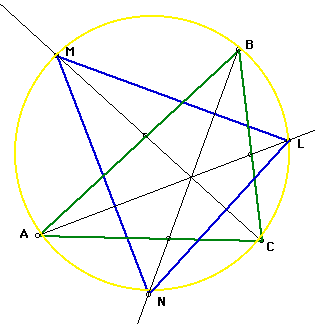
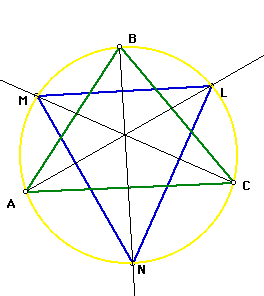
The angles that we created with our original triangle and our new triangle have different intercepted arcs. Are there any angles that have the same intercepted arc? If we can find any, then the angles will have the same measure. The following angles have the same intercepted arc:
Because of the construction of our original triangle ABC, we can substitute the following (remember the angles A,B, and C were bisected).
And
Therefore
Look at the image below to see the relationships above in the measurements. You can click on the image to download a GSP file. In the GSP file you can animate the image so that you can see the above relationship holds in various triangles.