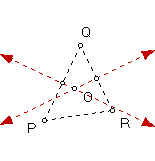
1. Prove the following theorems:
a. If P, Q, R are noncollinear, there is a unique circle C passing through P, Q, R.

Proof: Given points P, Q, R, construct the line segments PQ, QR, and PR. Construct the perpendicular bisectors of line segments QP and QR. Let the intersection of the perpendicular bisectors intersect at the point O. Since O is on the perpendicular bisector to QR, then d(OQ) = d(OR) by perpendicular bisector theorem. Also, since O is on the perpendicular bisector to QP, then d(OP) = d(OR) by perpendicular bisector theorem. So, d(OQ) = d(OP) = d(OR) by transitivity. So, O is equidistant to the points P, Q, R. Thus, there is a circle with center O passing through points P, Q, R by definition of a circle.
To prove uniqueness, suppose there is a circle with center O' that passes through the points P, Q, R. Then d(O'P) = d(O'R) = d(O'Q) by definition of a circle. Since d(O'R) = d(O'Q), then O' is on the perpendicular bisector to the line segment QR by perpendicular bisector theorem. Since d(O'P) = d(O'Q), then O' is on the perpendicular bisector to the line segment QP by perpendicular bisector theorem. Since O' lies on the perpendicular bisectors of line segments QR and QP, then O' is the intersection of the perpendicular bisectors of line segments QR and QP. Since O is the intersection of the perpendicular bisectors of line segments QR and QP, then O' = O. Thus, only one circle passes through the points P, Q, R. Therefore, if P, Q, R are noncollinear, there is a unique circle C passing through P, Q, R. QED.
b. If two tangents to a circle intersect, they make equal angles with the lines joining the point of intersection to the center, and the distances from the point of intersection to the two points of tangency are equal.
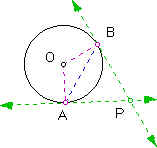
Proof: Given circle with center O and any points A and B on the circle such that A, O, B are not collinear (i.e., the two tangents intersect). m(OBP) = m(PAO) = 90 degrees by definition of a tangent to a circle.
Construct line segment AB. d(OA) = d(OB) by definition of a circle. So, m(BAO) = m(OBA) by isosceles triangle theorem. m(OBP) = m(OBA) + m(ABP) by angle measure theorem. So, m(ABP) = 90 degrees - m(OBA). m(PAO) = m(BAO) + m(PAB) by angle measure theorem. So, m(PAB) = 90 degrees - m(BAO) = 90 degrees - m(OBA) = m(ABP). Thus, d(AP) = d(BP) by isosceles triangle theorem. Therefore, if two tangents to a circle intersect, they make equal angles with the lines joining the point of intersection to the center, and the distances from the point of intersection to the two points of tangency are equal.
c. Through one of the points of intersection of two circles, chords are drawn through the centers of the circles. Prove that the line joining the ends of these chords passes through the other point of intersection of the circles.
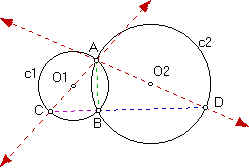
Proof: Given two circles c1 and c2 which intersect at two points A and B. Construct the lines O1A and O2A. Construct the intersection (point C) of line O1A with circle c1 and the intersection (point D) of line O2A with circle c2. Construct the line segments AB, CB and DB. m(DBA) = 1/2 m(arc DA) [by arc measure theorem] = 1/2(180 degrees) = 90 degrees. m(ABC) = 1/2 m(arc AC) [by arc measure theorem] = 1/2(180 degrees) = 90 degrees. So, m(DBC) = m(DBA) + m(ABC) [by angle measure theorem] = 90 degrees + 90 degrees = 180 degrees. So, points C, B, D are collinear by straight angle theorem. Therefore, if two circles intersect and if chords are drawn through the centers of two circles and the intersection of the circles, then the line joining the ends of these chords passes through the other point of intersection of the circles.
d. If P is a regular polygon, then there is a circle C such that all the vertices of P lie on C, and there is a circle D such that all the sides of P are tangent to D.
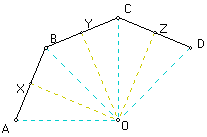
Proof: Given a regular polygon with n sides, n >= 3. Assume the polygon is convex. Construct the perpendicular bisector of each side. Construct the angle bisector of each angle. d(AX) = d(BX) since X is the midpoint of line segment AB. m(OXA) = -1*m(OXB) since line segment XO is on the perpendicular bisector of line segment AB. The angle bisectors of angle A and angle ABC intersect the perpendicular bisector of line segment AB at point O by the perpendicular bisector theorem. So, triangle AXO is similar to triangle BXO by SAS axiom. Since these triangles share the common side XO, triangle AXO is congruent to triangle BXO. Also, d(XB) = d(BY) since all sides of the polygons have equal length and X is the midpoint of line segment AB and Y is the midpoint of line segment BC. m(OBX) = -1*m(OBY) since line segment BO is on the angle bisector of angle XBY. Construct the line segment XY. Then the angle bisector of angle ABC is perpendicular to line segment XY by isosceles triangle theorem. Analogously, the angle bisector of angle BCD is perpendicular to the line segment YZ. So, the angle bisectors intersect at point O by perpendicular bisector theorem (as discussed above). So, triangle BXO is similar to triangle BYO by SAS axiom. Since these triangles share the common side BO, triangle BXO is congruent to triangle BYO. So, triangle AXO is congruent to triangle BYO by transitivity. Analogously, it is easy to show that the 2n triangles formed using the perpendicular bisectors and angle bisectors of the n-sided regular polygon are congruent. So, all the lengths d(OV), where V is a vertex of the regular n-gon, are congruent by definition of congruent. Thus, there is a circle C with center O which passes through the vertices of the regular n-gon, by definition of a circle. Also, all the lengths d(OM), where M is a midpoint of a side of the regular n-gon, are congruent by definition of congruent. Thus, there is a circle D with center O which passes through the midpoints of the sides of the regular n-gon, by definition of a circle. Since the line segment OM is perpendicular to the sides of the regular n-gon, the circle D is tangent to the sides by definition of tangent of a circle. Therefore, if P is a regular [convex] polygon, then there is a circle C such that all the vertices of P lie on C, and there is a circle D such that all the sides of P are tangent to D.
e. (extra credit) If two lines AB and CD intersect a circle in the four points A, B, C, D and have point P in common, then d(PA)d(PB) = d(PC)d(PD).
Proof:
Case I - P is outside circle.
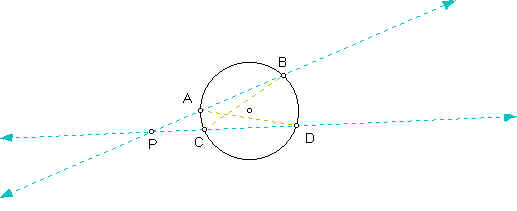
Given two lines AB and CD which intersect a circle at points A, B, C, D and have common point P which is outside the circle. m(CBA) = 1/2 m(arc CA) by arc measure theorem. Also, m(CDA) = 1/2 m(arc CA) by arc measure theorem. So, m(CBA) = m(CDA) by transitivity. m(CPB) = m(DPA) by angle measure theorem. So, triangle PAD is similar to triangle PCB by AA theorem. So, d(PC) = k*d(PA) and d(PB) = k*d(PD) by definition of similarity. This implies d(PC) = d(PA)*d(PB)/d(PD) by substitution. So, d(PC)d(PD) = d(PA)d(PB).
Case II - P is the center of the circle.
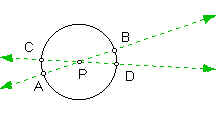
Given two lines AB and CD which intersect a circle at points A, B, C, D and have common point P which is the center of the circle. So, d(PA) = d(PB) = d(PC) = d(PD) by definition of a circle. So, d(PC)d(PD) = d(PA)d(PB).
Case III - P is inside the circle but not the center of the circle.
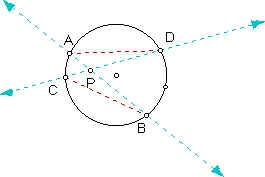
Given two lines AB and CD which intersect a circle at points A, B, C, D and have common point P which is inside the circle but is not the center of the circle. m(BAD) = m(BCD) because the subtend the same arc BD. m(PAD) = m(BAD) and m(BCP) = m(BCD) by angle measure theorem. m(ADC) = m(ABC) because the subtend the same arc AC. m(ADP) = m(ADC) and m(PCB) = m(ABC) by angle measure theorem. So, triangle ADP is similar to triangle CBP by AA theorem. So, d(PC) = k*d(PA) and d(PB) = k*d(PD) by definition of similarity. This implies d(PC) = d(PA)*d(PB)/d(PD) by substitution. So, d(PC)d(PD) = d(PA)d(PB).
Therefore, if two lines AB and CD intersect a circle in the four points A, B, C, D and have point P in common, then d(PA)d(PB) = d(PC)d(PD).
2. Suppose ray (PA) intersects a circle in two points A and B and ray (PC) intersects the circle in two points C and D. Find a relation between the measure of the angle APC and the angle measures of the arcs into which the points A, B, C, D divide the circle.
Conjecture: m(CPA) = 1/2 m(arc DB) - 1/2 m(arc AC).
Click here for a GSP sketch of the above conjecture. Be aware that as you move the rays, some of the arcs disappear - this is a shortcoming of GSP that I have not been able to find a way around.
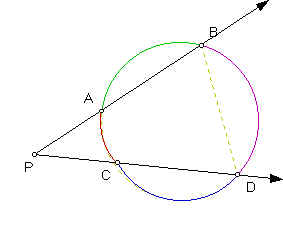
Proof: Given ray (PA) intersects a circle in two points A and B and ray (PC) intersects the circle in two points C and D. Construct the line segment BD. Consider the triangle PBD. So, m(DBP) + m(DPB) + m(BDP) = 180 degrees by triangle angle sum theorem. m(CPA) = m(DPB), m(BDC) = m(BDP) and m(DBA) = m(DBP) by angle measure theorem. m(DBA) = 1/2 m(arc ACD) [by inscribed angle theorem] = 1/2 (m(arc AC) + m(arc CD)) by angle measure theorem. Analogously, m(BDC) = 1/2 m(arc BAC) [by inscribed angle theorem] = 1/2 (m(arc AC) + m(arc BA)) by angle measure theorem. So, by substitution, we have m(DBP) + m(CPA) + m(BDP) = m(CPA) + 1/2 (m(arc AC) + m(arc CD)) + 1/2 (m(arc AC) + m(arc BA)) = 180 degrees. But 180 degrees = 1/2*360 degrees = 1/2 (m(arc AC) + m(arc CD) + m(arc DB) + m(arc BA)). So, by substitution, we have m(CPA) + 1/2 (m(arc AC) + m(arc CD)) + 1/2 (m(arc AC) + m(arc BA)) = 1/2 (m(arc AC) + m(arc CD) + m(arc DB) + m(arc BA)). So, m(CPA) = 1/2 (m(arc AC) + m(arc CD) + m(arc DB) + m(arc BA)) - [1/2 (m(arc AC) + m(arc CD)) + 1/2 (m(arc AC) + m(arc BA))] = 1/2 m(arc DB) - 1/2 m(arc AC). Therefore, if ray (PA) intersects a circle in two points A and B and ray (PC) intersects the circle in two points C and D, then m(CPA) = 1/2 m(arc DB) - 1/2 m(arc AC).
Extension #1:
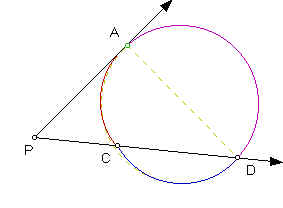
Given ray (PA) intersects a circle at point A and ray (PC) intersects the circle in two points C and D. Construct the line segment AD. Consider the triangle PAD. So, m(DAP) + m(DPA) + m(ADP) = 180 degrees by triangle angle sum theorem. m(CPA) = m(DPA), m(ADC) = m(ADP) by angle measure theorem. m(DAP) = 1/2 m(arc ACD) [by inscribed angle theorem] = 1/2 (m(arc AC) + m(arc CD)) by angle measure theorem. Analogously, m(ADC) = 1/2 m(arc AC) [by inscribed angle theorem]. So, by substitution, we have m(DAP) + m(CPA) + m(ADC) = m(CPA) + 1/2 (m(arc AC) + m(arc CD)) + 1/2 (m(arc AC)) = 180 degrees. But 180 degrees = 1/2*360 degrees = 1/2 (m(arc AC) + m(arc CD) + m(arc DA)). So, by substitution, we have m(CPA) + 1/2 (m(arc AC) + m(arc CD)) + 1/2 (m(arc AC)) = 1/2 (m(arc AC) + m(arc CD) + m(arc DA)). So, m(CPA) = 1/2 (m(arc AC) + m(arc CD) + m(arc DA)) - [1/2 (m(arc AC) + m(arc CD)) + 1/2 (m(arc AC))] = 1/2 m(arc DA) - 1/2 m(arc AC). Therefore, if ray (PA) intersects a circle at point A and ray (PC) intersects the circle in two points C and D, then m(CPA) = 1/2 m(arc DA) - 1/2 m(arc AC).
Extension #2:
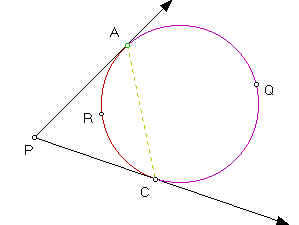
Given ray (PA) intersects a circle at point A and ray (PC) intersects the circle at point C. Construct the line segment AC. Consider the triangle PAC. So, m(CAP) + m(CPA) + m(ACP) = 180 degrees by triangle angle sum theorem. m(CAP) = 1/2 m(arc ARC) by inscribed angle theorem. Analogously, m(ACP) = 1/2 m(arc ARC) by inscribed angle theorem. So, by substitution, we have m(CAP) + m(CPA) + m(ACP) = m(CPA) + 1/2 m(arc ARC) + 1/2 m(arc ARC) = 180 degrees. But 180 degrees = 1/2*360 degrees = 1/2 (m(arc ARC) + m(arc CQA)). So, by substitution, we have m(CPA) + 1/2 m(arc ARC) + 1/2 m(arc ARC) = 1/2 (m(arc ARC) + m(arc CQA)). So, m(CPA) = 1/2 (m(arc ARC) + m(arc CQA)) - [1/2 m(arc ARC) + 1/2 m(arc ARC)] = 1/2 m(arc CQA) - 1/2 m(arc ARC). Therefore, if ray (PA) intersects a circle at point A and ray (PC) intersects the circle at point C, then m(CPA) = 1/2 m(arc CQA) - 1/2 m(arc ARC).