4. Given two points A and B, construct a square with diagonal AB.
Click here for a GSP sketch of the constructed square.
Click here for a JSP sketch of the constructed square. NOTE: you will need a java-enabled browser.
Construction:

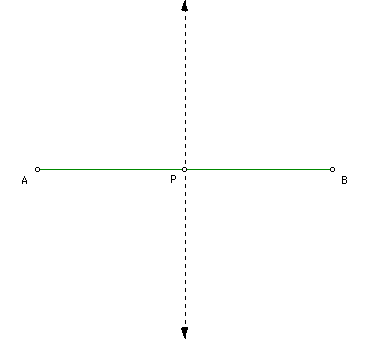
Given diagonal AB. The lemma below states that the diagonals of a square are perpendicular bisectors. So, the first step is to construct the other diagonal by constructing the perpendicular bisector [see lemma below].
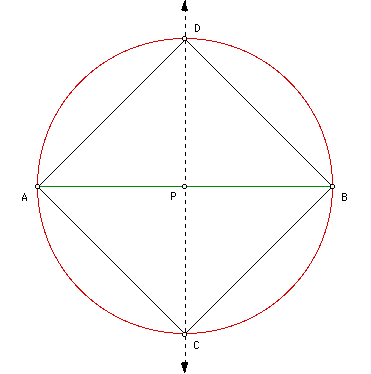
The lemma also states that the diagonals bisect each other. In other words, the distances from P to each vertex are congruent. Two vertices of the square are known: points A and B. So, to construct the other two vertices, we construct a circle with center at point P with radius of length d(PA). The last two vertices (points C and D) are found at the intersection of the circle and the perpendicular bisector.
LEMMA: Given a square ABCD, the diagonals are perpendicular bisectors of each other. See Proof.