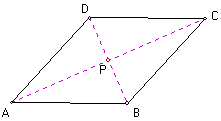
LEMMA: the diagonals of a
rhombus are perpendicuar bisectors of each other.
Proof: Point B is equidistant to point A and point B since ABCD is a rhombus. So, point B lies on the perpendicular line to segment AC by the perpendicular bisector theorem. Analogously, point D lies on the perpendicular line to segment AC by the perpendicular bisector theorem. These two perpendicular bisectors are the same line by the uniqueness of the perpendicular bisector. So, d(AP) = d(PC). Analogously, it is easy to show d(BP) = d(PC). QED
Angle APB is congruent to angle APD since they are right angles. So, triangle APB is similar to triangle APD by SAS axiom. Since both triangles contain the same side (AP), triangle APB is congruent to triangle APD. Analogously, it is easy to show triangle CPB is similar to triangle CPD and it is easy to show triangle BPA is similar to triangle BPC. Thus, the four triangles (APB, APD, CPB, and CPD) are congruent by transitivity.

Draw the line perpendicular to side AD through point P. Suppose this line intersects segment AD at point E and it intersects segment BC at point F. So, angle PED is a right angle and is congruent to angle PFC by alternating interior angle theorem. So, angle PFB is a right angle since angle BFC is a straight angle and is formed by the two angles PFB and PFC. Angle PDE is congruent to angle PBF by alternating interior angle theorem. So, triangle PED is similar to triangle PFB by angle angle theorem. So, triangle PED is congruent to triangle PFB since d(PD) = d(PB). Thus, d(PE) = d(PF) becasue corresponding parts of congruent triangles are congruent. Analogously, it is easy to show d(PG) = d(PH).
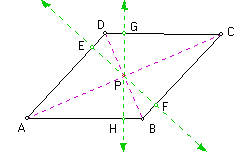
Angle ADP is congruent to angle PBF by alternating interior angle theorem. Angle APD is congruent to angle PFB since they are both right angles. Thus, triangle APD is similar to triangle PFB by angle angle theorem. Analogously, it is easy to show that triangle APB is similar to triangle PGD by angle angle theorem. So, triangle PGD is similar to triangle PFB by angle angle theorem. So, triangle PGD is congruent to triangle PFB, since d(PD) = d(PB). Analgously, it is easy to show that the four triangles (PGD, PED, PFB, and PHB) are all congruent. Thus, d(PG) = d(PE) = d(PF) = (PH) because corresponding parts of congruent triangles are congruent.
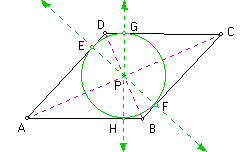
Thus, the segments PG, PE, PF, and PH have the same length and are perpendicular to a side of the rhombus. Thus, a circle with center at point P with radius = d(PG) will be tangent to each side of the rhombus.