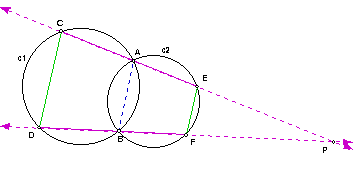
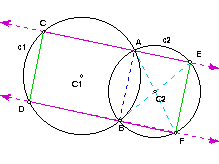
2. Theorem: Suppose that two circles c1 and c2 intersect in two points A and B. Suppose that C and D are points on C1, and E and F are points on c2, such that A lies on the line segment CE and B lies on the line segment DF. Prove that the lines CD and EF are parallel.
Proof: Suppose that two circles c1 and c2 intersect in two points A and B. Suppose that C and D are points on C1, and E and F are points on c2, such that A lies on the line segment CE and B lies on the line segment DF. I have proven the following theorem in HW 7: if two lines QR and ST intersect a circle in the four points Q, R, S, T and have point P in common, then d(PQ)d(PR) = d(PS)d(PT).
Case 1: Suppose the line passing through points CE and the line passing through points DF intersect at point P.

Since the lines CE and DF intersect the circle c1 in the four points C, A, D, B, and have point P in common, then d(PC)d(PA) = d(PD)d(PB) by the above theorem.
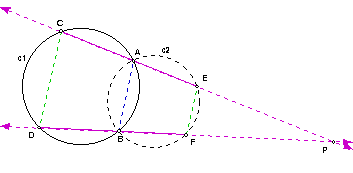
Since the lines CE and DF intersect the circle c2 in the four points A, E, B, F, and have point P in common, then d(PA)d(PE) = d(PB)d(PF) by the above theorem.
Since d(PC)d(PA) = d(PD)d(PB) and d(PA)d(PE) = d(PB)d(PF), then d(PA)/d(PB) = d(PD)/d(PC) and d(PA)/d(PB) = d(PF)/d(PE). So, d(PD)/d(PC) = d(PF)/d(PE) = k by transitivity, where k = d(PA)/d(PB). So, (d(PC)/d(PF))*(d(PD)/d(PC) = d(PF)/d(PE) = k) which implies d(PD)/d(PF) = d(PC)/d(PE) = k' where k' = d(PA)d(PC)/d(PB)d(PF). So, d(PD) = k'*d(PF) and d(PC) = k'*d(PE).
In addition, m(EPF) = m(CPD) by angle measure theorem. So, triangle EPF is similar to triangle CPD by SAS Axiom. So, m(DCP) = m(FEP) by definition of similarity. So, line CE is parallel to line EF by transversal theorem.
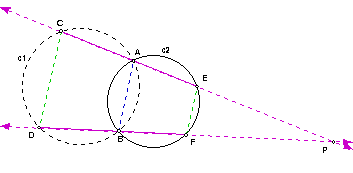
Case 2: Suppose the line passing through points CE and the line passing through points DF do not intersect.
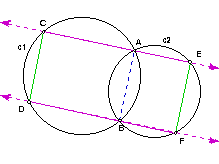
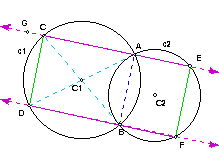
CE and DF are parallel since they do not intersect [by definition of parallel]. Consider the circle, c2 with center C2. m(AEB) = m(FBE) by alternate interior angle theorem. Since m(AEB) = 1/2 m(arc(AB)) and m(FBE) = 1/2 m(arc(EF)) by the inscribed angle theorem, then m(arc(AB)) = m(arc(EF)) by transitivity [note: all arcs will be assumed to be minor arcs unless otherwise described]. Also, m(FAE) = m(AFB) by alternate interior angle theorem. So, triangle AEC2 is similar to triangle FBC2 by the angle-angle theorem. So, m(AC2E) = m(FC2B) by definition of similarity. Since m(AC2E) = 1/2 m(arc(AE)) and m(FC2B) = 1/2 m(arc(BF)) by the inscribed angle theorem, then m(arc(AE)) = m(arc(BF)) by transitivity. So, m(AEF) = 1/2 m(arc(ABF)) [by the inscribed angle theorem] = 1/2 m(arc(AB) + arc(BF)) [by definitions of arc] = 1/2 m(arc(EF) + arc(AE)) [by substitution] = 1/2 m(arc(AEF)) [by definitions of arc] = m(FBA) [by the inscribed angle theorem]. Analogously, it is easy to show m(BAE) = m(EFB). So, m(BAE) = m(BAF) + m(FAE) [by angle measure theorem] =1/2 m(arc(BF)) + 1/2 m(arc(EF)) [by the inscribed angle theorem] = 1/2 m(arc(AE)) + 1/2 m(arc(AB)) [by substitution] = m(EFA) + m(AFB) [by the inscribed angle theorem] = m(EFB) by angle measure theorem. So, m(BAE) = m(EFB). Analogously, it is easy to show m(AEF) = m(FBA).
Analogously, for circle c1, it is (somewhat!) easy to show m(DCA) = m(ABD) and m(CAB) = m(BDC) using a similar argument as was made for circle c2. Also, m(ABD) = m(BAE); m(BDC) = m(GCD); m(CAB) = m(FBA) by alternate interior angle theorem. So, m(AEF) = m(FBA) [from above paragraph] which implies m(AEF) = m(CAB) [by substitution] which implies m(AEF) = m(BDC) [by substitution] which implies m(AEF) = m(GCD). Since m(AEF) = m(GCD), then DC is parallel to EF by transversal theorem. QED
Return to geometry page