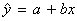 , where
, where 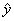 (called "y hat") is the predicted value for the response variable. Because of the scatter of
points about the line, the predicted response will usually not be exaclty the same as the actually observed
response y.
(called "y hat") is the predicted value for the response variable. Because of the scatter of
points about the line, the predicted response will usually not be exaclty the same as the actually observed
response y.Correlation measures the direction and strength of the 'linear' relationship between two quantitative variables. If a scatterplot shows a linear relationship, we would like to describe it with an equation of a line (a mathematical model of the relationship). The regression line summarizes the relationship between an explanatory and response variable. We often use the regression line to predict the value of the response variable for a given value of the explanatory variable. There are some dangers to predicting that we will cover in section 2.4.
We need a method for constructing a regression line that will be consistent for all looking at the data. Here is a good website that shows how close your guess at the regression line is to the line constructed by the method of least squares. This is an excellent way to develop a feel for linear regression!
The least–squares regression line of y on x is the line that makes the sum of the squares
of the deviations of the data points from the line in the vertical direction as small as possible.
The least-squares regression line is the line 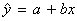 , where
, where 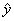 (called "y hat") is the predicted value for the response variable. Because of the scatter of
points about the line, the predicted response will usually not be exaclty the same as the actually observed
response y.
(called "y hat") is the predicted value for the response variable. Because of the scatter of
points about the line, the predicted response will usually not be exaclty the same as the actually observed
response y.
Here are steps to find the least–squares regression line using the TI-83 calculator.
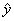 . Otherwise, a change in the x–variable results in a
smaller change in
. Otherwise, a change in the x–variable results in a
smaller change in 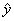 .
.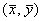 .
.A residual is the difference between an observed value of the response variable and the value predicted
by the regression line:
Residuals (prediction error) = observed y – predicted y =
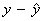 .
.
There are residuals for each data point. Residuals are positive when the data point is above the regression line and residuals are negative when the data point is below the regression line.
Because the residuals show how far the data fall from our regression line, examining the residuals helps assess how well the line describes the data. The mean of the residuals from the least–squares regression line is always zero. A residual plot is a scatter plot of the regression residuals against the explanatory variable. Residual plots also help us ass the fit of a regression line.
Here are steps to finding and graphing the residuals using the TI-83 calculator.
Here are some key things to consider when examining the residual plot (see pp. 118–121 of your text for example graphs of each of the key ideas below):
An outlier is a observation that lies far from the fitted line and so produces a large residual. This observation is an outlier in the y direction.
An observation is influential if removing it would markedly change the position of the regression line. This observation is an outlier in the x direction.