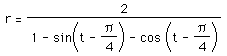The purpose of this exploration is to investigate polar equations and
their graphs. We may use Theorist to graph functions such as
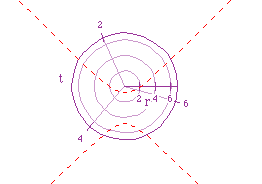
The following is a graph of the polar equation above.
It appears as thought the equation graphs as an ellipse. Specifically, this ellipse's major axis lies along the angle t = 0. Now, let's investigate several other equations. Let's begin with
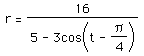
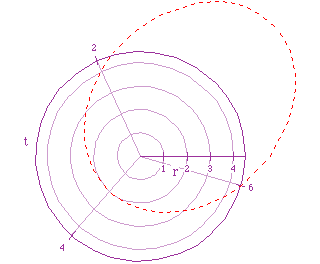
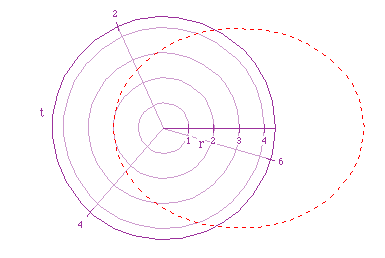
Notice that the graph greatly resembles the graph of the first equation;
however, we can easily see that this new graph is somewhat "tilted."
For this reason, the major axis will tilt as well. In fact, the major axis
now coincides with with the angle t= 
. The "tilt" is more
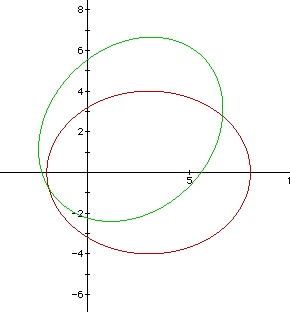
obvious if we view these graphs together.
Let's try altering the equation again. One might conjecture that the constant that appears after the angle affects the "tilt" of the graph. Does it follow that an equation such as
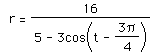
would have its major axis coincide with the angle t = 
, which is located
in the second quadrant? Let's view the graph of this equation as well as
the graphs of the previous two equations.
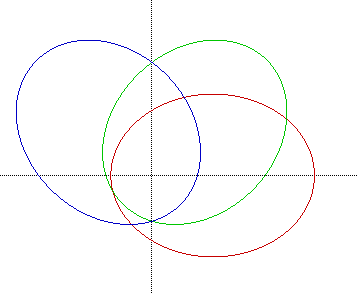
Our expectations are correct. Our findings may be generalized to include that any equation of the form
,where c is some real number, is simply an ellipse whose major axis coincides with angle t = c.
Now, let's examine the equation
.
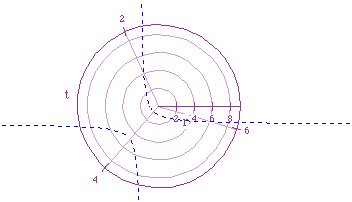
This time, the graph seems to be a hyperbola which is asymptotic to the x-axis. Now, let's examine several other functions. Begin with
