ASSIGNMENT # 2


PROBLEM # 8

Let's examine the quadratic function

and vary the values of d. In particular, we want to decide whether or not varying the values of d will change the general shape and/or position of the graph. We will begin by examining the function

which we will call the "parent" graph for our quadratic functions.


Notice that the "parent" graph is simply a parabola whose vertex is located at the origin.

At this point we wish to examine what happens when we graph

,

where d = 0.

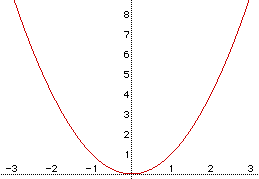
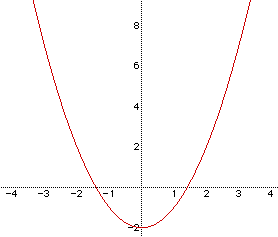
Notice that if d = 0, the rule would be

and the graph moves down the y-axis two units.


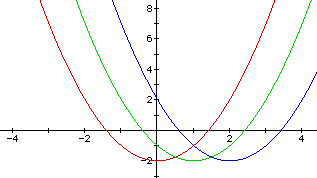
Now, let's look at the case where d = 1 and when d = 2. Hence, the equation would be

and

.

Again, our "parent" graph's vertex remains at the point (0,-2), the green parabola represents the function

and the parabola has its vertex at the point (1,-2). The blue parabola is a graph of the function

with a vertex of (2,2). It would appear as though the y-coordinate of the parabola has remain unchanged, whereas the x-coordinate has moved one unit to the right each time we increase d by 1. It follows that as d increases, the graph moves d units to the right when d is positive.

Now, what happens when d is some negative value? Will the graph move to the left? Let's begin by allowing d = -3. Hence, our equation would be

or

.

Let's compare the "parent" with our new rule:

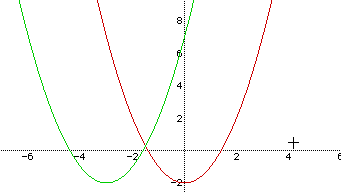
As before, our red parabola represents our "parent" and the green parabola represents our rule

.

Again, as we allowed d to be negative, the vertex of the parabola moved d units to the left.


CONCLUSIONS

One may easily see from the graphs above that the general shape and direction of the parabola remained unchanged, whereas the position of the parabola's vertex along the x-axis changed depending on the chosen value of d. Indeed, the parabola moves d units to the right if d is some positive real number and the parabola moves d units to the left if d is some negative real number.

Return to Brian Wynne's Class Page