The exercise of constructing a graph for the equation
has been made easier with the availability of instructional technology. Indeed, students may use application programs such as Algebra Xpresser to complete investigations for different values of a, b, or c as the other two variables are held constant when
Let's begin by allowing a to remain 1 and allow c to remain 1 while varying
the values of b. Suppose b = -3, -2, -1, 0, 1, 2, 3. If we examine the graphs
below, some rather interesting patterns are developed.
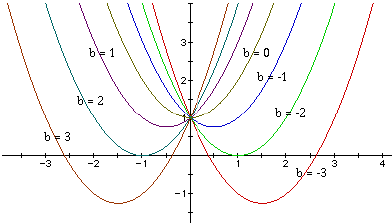
It should be rather easy to formulate several conjectures as to the "movement"of the parabola as b changes. It would be wise to first discuss the nature of the roots. Notice that if b = 3 or b = -3, there are two x-intercepts (or two roots); if b = 2 or b = -2 then the parabola is tangent to the x-axis and only has one root (referred to as a double root); if b = 1 or b = -1 or b = 0 , the parabolas never cross the x-axis and this implies that there are two imaginary roots. Nonetheless, every quadratic equation will have two roots--either two real roots, two imaginary roots, or a single real root (which mathematicians refer to as a double root). It is important to stress the concept of x-intercepts due to the fact when students solve equations, they are finding the roots, which is a synonym for x-intercepts.
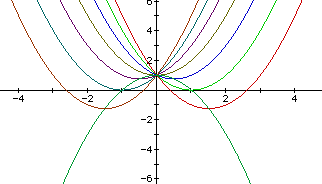
The locus of the vertices of the parabolas is given by the equation
and is shown above as the parabola that opens in a downward direction. In an attempt to generalize, the two constant terms are the same and the coefficients of the quadratic terms only differ by a sign.
Now, it is necessary to consider
in the xb plane. We would get a graph that resembles the following.
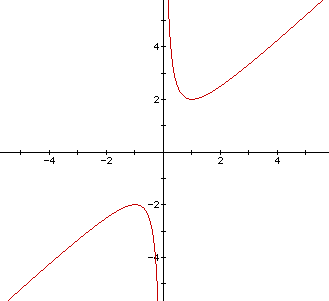
This is the resulting graph if b = 0. Consider other values of b--such as b = 1, b = 2, b = -1 , b = -2.
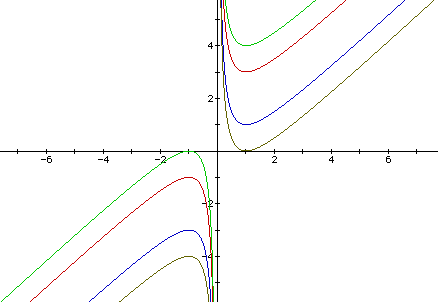
The red graph is the result of b = 1, the green graph is the result of b = 2, the blue graph is the result of b = -1, and the gold graph is the result of b = -2. Notice that when b = 1, the graph moves one unit up along the b-axis, when b = 2 the graph moves two units up along the b-axis, etc.. If b < 0, then the graph moves b units down along the b-axis.
Now, suppose we choose some particular value of b, say b = 3, and overlay this equation on the graph. The result is a line parallel to the x-axis. If it intersects the curve in the xb-plane, then the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.
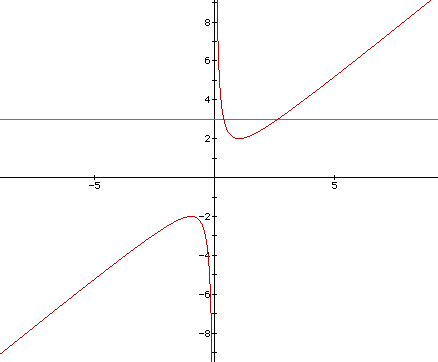
Indeed, for each value of b that we select, we get a horizontal line. It is quite clear on a single graph that we get two positive real roots. In fact, if b > 2, there are two positive real roots; if b < -2, there are two negative real roots; if -2 < b < 2, there are no real roots. Now, consider the following two cases: 1) If b = 2, then there is one positive real root; 2) if b = -2, then there is one negative real root.
Now consider the relation
and allow b = 0. In addition, we will allow c = -1 as opposed to c = 1--as we prior to this section.
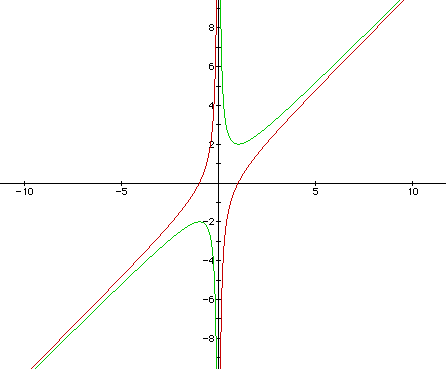
Notice that the green graph is the original relation when c = 1, and the red graph is the relation when c = -1. The red graph is "asymptotic" to the green graph.
We shall now consider the equation
and its graph in the xc-plane. Obviously, the curve will be a parabola. For each value of c considered, the graph will be a line crossing the parabola in 0, 1, or 2 points--the intersections being at the roots of the original equation at that value of c. Let's begin by considering the case when c = 1. Hence, the equation is
and we will consider the horizontal line c = 1.
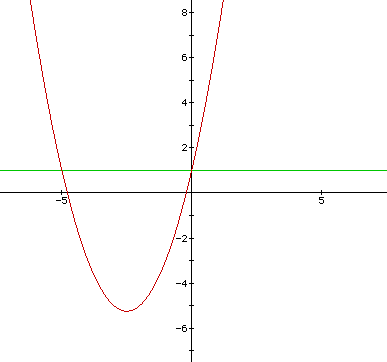
Hence, the two roots are {-.2,-4.8} when we are looking for the x-inercepts. However, the roots are {-5,0} if c = 1. Consider the case when c = 2.
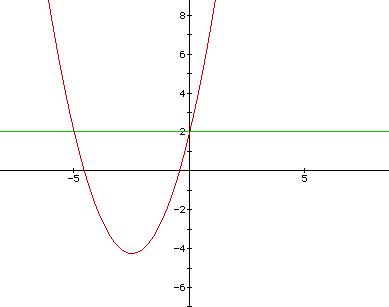
Once again, if we examine the the points of intersection of the parabola with the line c = 2, we see that the roots are {0,-5}--the same as before. Indeed, if we continue to choose the same value of c in the relation as we do to graph the horizontal line, then the roots will continue being the same.