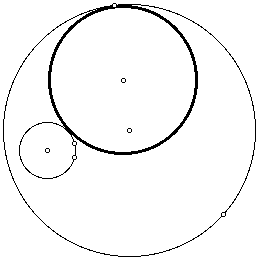

At this point, we shall also construct an isosceles triangle with vertices
at the center of the large circle, the center of one of the small circles,
and one endpoint of the diameter of the second small circle. Our picture
would then resemble the following.
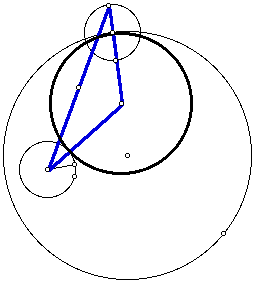
Next, we want to trace the the center of the large circle and examine
the locus of points created by the trace.
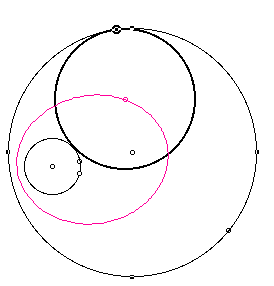
It appears as though the shape that the point traces out is an ellipse.
In order to see a complete animation,
It is also possible to animate the base of the isosceles triangle and
make note of whether or not the animation provides us with the same figure.

Just as we saw before, the figure is an ellipse.
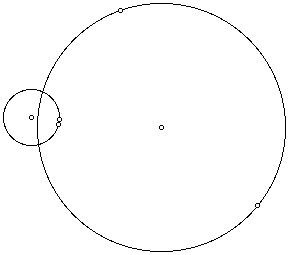
At this point we also wish to discuss the construction of tangent circles
if the two given circles intersect. The picure below depicts the situation.
Next, we must trace the center of the larger, tangent circle.
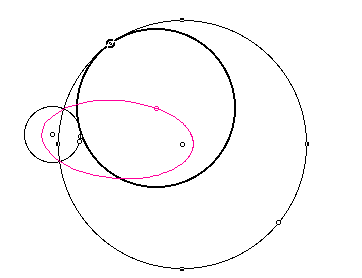
Furthermore, we may also animate the segments from the centers of the
given circles to the tangent circles and make any necessary observations.

Again, our end product appears to be an ellipse. If you wish to see
the animation,