

In order to fold the sides to make the box, it is necessary to cut out
squares from each corner.
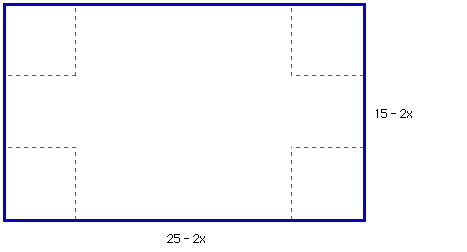
In the picture above, the length of each side of the square measures
x. Originally, the length of the rectangular piece of cardboard was
25 inches; however, if we cut a section measuring x from one corner
and a second section measuring x from the other corner, we have essentially
removed 2x from the 25 inches. It follows that the "new"
length of the rectangular region is 25 - 2x. Similarly, the width
of the rectangular region is now 15 - 2x.
Of course, we must know a value of x in order to calculate the volume.
Suppose that x = 2. This means that the square region we are removing has
a side measuring 2 inches. Using the formula, we see that
Unfortunately, this formula will not generate the maximum area without
going through a great deal of trial-and-error. However, we may use a spreadsheet,
such as EXCEL, to examine different values of x and the volume that a particular
value of x will yield. Although we wish to create an extensive list, we
should also keep in mind that upon examining these values, x may have to
be restricted. Let's begin by booking at values of x in the interval [1,30].
x | 25-2x | 15-2x | Volume |
| 1 | 23 | 13 | 299 |
| 2 | 21 | 11 | 462 |
| 3 | 19 | 9 | 513 |
| 4 | 17 | 7 | 476 |
| 5 | 15 | 5 | 375 |
| 6 | 13 | 3 | 234 |
| 7 | 11 | 1 | 77 |
| 8 | 9 | -1 | -72 |
| 9 | 7 | -3 | -189 |
| 10 | 5 | -5 | -250 |
| 11 | 3 | -7 | -231 |
| 12 | 1 | -9 | -108 |
| 13 | -1 | -11 | 143 |
| 14 | -3 | -13 | 546 |
| 15 | -5 | -15 | 1125 |
| 16 | -7 | -17 | 1904 |
| 17 | -9 | -19 | 2907 |
| 18 | -11 | -21 | 4158 |
| 19 | -13 | -23 | 5681 |
| 20 | -15 | -25 | 7500 |
| 21 | -17 | -27 | 9639 |
| 22 | -19 | -29 | 12122 |
| 23 | -21 | -31 | 14973 |
| 24 | -23 | -33 | 18216 |
| 25 | -25 | -35 | 21875 |
| 26 | -27 | -37 | 25974 |
| 27 | -29 | -39 | 30537 |
| 28 | -31 | -41 | 35588 |
| 29 | -33 | -43 | 41151 |
| 30 | -35 | -45 | 47250 |
It is important to note that if we use values of x greater than or equal
to 7.5, then the width (given as 15 - 2x) will either be 0 or will be negative.
Obviously, if the width is 0 this reduces our figure to a two-dimensional
object; if the width is negative, this situation is impossible. Hence, x
must be less than 7.5. In addition, x must be greater than 0 because we
do not want to choose a height of 0 or a negative height.
Now that it has been stipulated that x is in the interval (0, 7.5), we may
now examine the chart for the maximum volume. Notice that if x = 2, then
the volume = 462 cubic inches; if x = 3, then the volume = 513 cubic inches.
However, if x = 4, then the volume = 476 cubic inches. So, it appears as
though the maximum volume is produced when x = 3. Unfortunately, this chart
only reveals integral values of x. It is certainly possible that the maximum
volume could be produced for some value of x between 3 and 4. Let's explore
some of those values.
x | 25 - 2x | 15 - 2x | Volume |
| 3 | 19 | 9 | 513 |
| 3.01 | 18.98 | 8.98 | 513.025604 |
| 3.02 | 18.96 | 8.96 | 513.042432 |
3.03 | 18.94 | 8.94 | 513.050508 |
| 3.04 | 18.92 | 8.92 | 513.049856 |
| 3.05 | 18.9 | 8.9 | 513.0405 |
| 3.06 | 18.88 | 8.88 | 513.022464 |
| 3.07 | 18.86 | 8.86 | 512.995772 |
| 3.08 | 18.84 | 8.84 | 512.960448 |
| 3.09 | 18.82 | 8.82 | 512.916516 |
| 3.1 | 18.8 | 8.8 | 512.864 |
| 3.11 | 18.78 | 8.78 | 512.802924 |
| 3.12 | 18.76 | 8.76000000000001 | 512.733312 |
| 3.13 | 18.74 | 8.74000000000001 | 512.655188 |
| 3.14 | 18.72 | 8.72000000000001 | 512.568576 |
| 3.15 | 18.7 | 8.70000000000001 | 512.4735 |
| 3.16 | 18.68 | 8.68000000000001 | 512.369984 |
| 3.17 | 18.66 | 8.66000000000001 | 512.258052 |
| 3.18 | 18.64 | 8.64000000000001 | 512.137728 |
| 3.19 | 18.62 | 8.62000000000001 | 512.009036 |
| 3.2 | 18.6 | 8.60000000000001 | 511.872 |
Notice that the chart reveals that if x = 3.03, then the maximum volume
is approximately 513.05 cubic inches.
We also want to know the size(s) of the box that would produce a volume
of 400 cubic inches. If we look at the original spreadsheet above, we can
easily see that if x = 1, then the volume is 299 cubic inches; if x = 2,
then the volume is 462 cubic inches. It follows that the value of x that
would produce such a box is in the interval (1,2). Let's explore these values
further.
| 1.52 | 21.96 | 11.96 | 399.215232 |
| 1.53 | 21.94 | 11.94 | 400.804308 |
This small portion of the chart reveals that x must be between 1.52 and
1.53. So, let's explore a bit further.
| 1.52492010000003 | 21.9501597999999 | 11.9501597999999 | 399.99861539686 |
| 1.52493010000003 | 21.9501397999999 | 11.9501397999999 | 400.000204564287 |
| 1.52494010000003 | 21.9501197999999 | 11.9501197999999 | 400.001793719374 |
Notice that if x = 1.5249301, then the volume is approximately 400 cubic
inches.
We should also note that if x = 4, then the volume of the box is 476 cubic
inches and if x = 5, the volume is 375 cubic inches. Hence, a second value
of x will yield a volume of 400 cubic inches as well and that value is located
in the interval from (4,5). Let's examine those values.
| 4.7910000000001 | 15.4179999999998 | 5.41799999999981 | 400.214862683989 |
| 4.7920000000001 | 15.4159999999998 | 5.4159999999998 | 400.098724351989 |
| 4.7930000000001 | 15.4139999999998 | 5.4139999999998 | 399.982541027989 |
Again, this is only a small portion of the spreadsheet, however it seems
as though if x is approximately 4.79 inches, then the volume of the box
would be 400 cubic inches.
represents the volume of the lidless box for given values of x. Now,
let's take this same function and graph it.
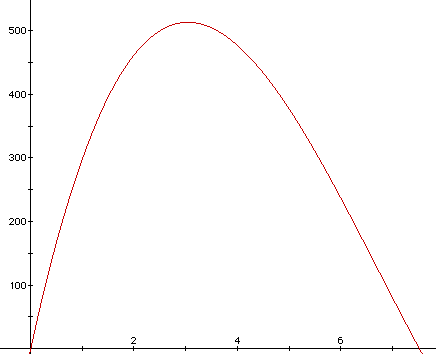
Although the graph of the volume function would typically as a cubic
function, we only want to view the portion of the graph where x is the interval
from (0,7.5)--as we stated earlier. Hence, this portion of the graph appears
to be an upside down parabola. The x-axis represents the length of a side
of the square in inches, and the y-axis represents the volume of the rectangular
box. Moreover, the vertex will provide us with the needed information; i.e.,
the x-coordinate will tell us the required length of one side of the box
in order to yield the maximum volume (y-coordinate of the vertex). Let's
try to look at a close-up picture of the vertex of this parabola.
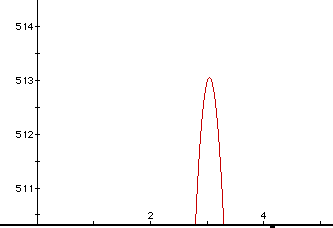
Just "eyeballing" this picture it appears as though the vertex
is given by the point (3.0,513). It follows that we must cut-out a square
with a side measuring approximately three inches or so in order to obtain
a box whose volume is approximately 513 cubic inches.
Let's also try to find the size(s) of the square that would produce a box
volume of 400 cubic inches. Indeed, we are looking for points on the graph
where the y-coordinate is 400. We may visually locate these points by drawing
the line y =400 and looking for points of intersection with the volume function.
Again, we will place the same restrictions on x as before.
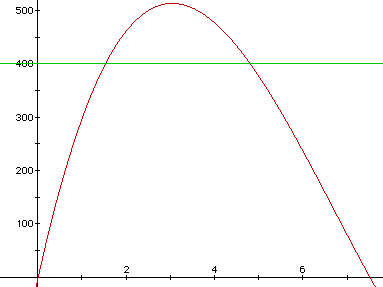
Notice that the horizontal line y = 400 intersects the volume function
in two points, so there are two values of x that will produce a box of the
desired volume. At this point, it is necessary to focus on those two points
of intersection.
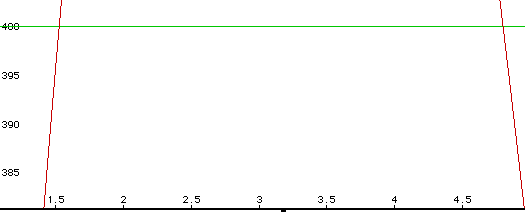
It appears as though x = 1.5 or x = 4.7 would yield a box whose volume
is 400 cubic inches. Obviously, these are approximate values.
In order to be as accurate as possible, it is necessary to multiply by
the appropriate scale factor for the drawing. Indeed, the results should
be the same: 1) the maximum volume of the box is approximately 513 cubic
inches and 2) x should be approximatley 1.5 or approximately 4.7 in order
to construct a box whose volume is 400 cubic inches.